
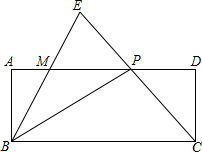
 已知如图,在矩形ABCD中,P是边AD上的一动点,连结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD与点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x(2<x≤5),PM=y
已知如图,在矩形ABCD中,P是边AD上的一动点,连结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD与点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x(2<x≤5),PM=y分析 (1)证明△ABM∽△APB,得出对应边成比例,即可得出y关于x的函数解析式;
(2)过点M作MH⊥BP于H,由AP=x=4,可求出MP、AM、BM、BP,再根据面积法求出MH,从而求出BH,即可求出∠EBP的正切值;
(3)分两种情况讨论:①当EB=EC时,可证△AMB≌△DPC,则有AM=DP,从而有x-y=5-x,即y=2x-5,代入(1)中函数解析式就可求出x的值;
②当CB=CE时,得到PC=EC-EP=BC-MP=5-y,在Rt△DPC中根据勾股定理可得到x与y的关系,然后结合y关于x的函数解析式,解方程求出x的值.
解答 解:(1)∵四边形ABCD是矩形,
∴AB=CD=2,AD=BC=5,∠A=∠D=90°,AD∥BC,
∴∠APB=∠PBC.
∵∠ABE=∠CBP,
∴∠ABM=∠APB.
又∵∠A=∠A,
∴△ABM∽△APB,
∴$\frac{AB}{AP}$=$\frac{AM}{AB}$,
即$\frac{2}{x}$=$\frac{x-y}{2}$,
∴y=x-$\frac{4}{x}$(2<x≤5);
(2)过点M作MH⊥BP于H,如图所示: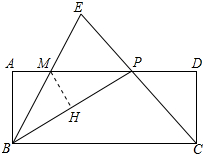 ∵AP=x=4,
∵AP=x=4,
∴y=x-$\frac{4}{x}$=3,
∴MP=3,AM=1,
∴BM=$\sqrt{A{B}^{2}+A{M}^{2}}$=$\sqrt{5}$,BP=$\sqrt{A{B}^{2}+A{P}^{2}}$=2$\sqrt{5}$,
∵△BMP的面积=$\frac{1}{2}$MP•AB=$\frac{1}{2}$BP•MH,
∴MH=$\frac{MP•AB}{BP}$=$\frac{3\sqrt{5}}{5}$,
∴BH=$\sqrt{B{M}^{2}-M{H}^{2}}$=$\frac{4\sqrt{5}}{5}$,
∴tan∠EBP=$\frac{MH}{BH}$=$\frac{3}{4}$;
(3)分两种情况:
①若EB=EC,
则∠EBC=∠ECB.
∵AD∥BC,
∴∠AMB=∠EBC,∠DPC=∠ECB,
∴∠AMB=∠DPC.
在△AMB和△DPC中,
$\left\{\begin{array}{l}{∠AMB=∠DPC}&{\;}\\{∠A=∠D}&{\;}\\{AB=DC}&{\;}\end{array}\right.$,
∴△AMB≌△DPC,
∴AM=DP,
∴x-y=5-x,
∴y=2x-5,
∴x-$\frac{4}{x}$=2x-5,
解得:x1=1,x2=4.
∵2<x≤5,
∴AP=x=4;
②若CE=CB,
则∠EBC=∠E.
∵AD∥BC,
∴∠EMP=∠EBC=∠E,
∴PE=PM=y,
∴PC=EC-EP=5-y,
∴在Rt△DPC中,
(5-y)2-(5-x)2=22,
∴(10-x-y)(x-y)=4,
∴(10-x-x+$\frac{4}{x}$)(x-x+$\frac{4}{x}$)=4,
整理得:3x2-10x-4=0,
解得:x=$\frac{5±\sqrt{37}}{3}$(负值舍去),
∴AP=x=$\frac{5+\sqrt{37}}{3}$;
综上所述:AP的值为:4或$\frac{5+\sqrt{37}}{3}$.
点评 本题是四边形综合题目,考查了相似三角形的判定与性质、全等三角形的判定与性质、矩形的性质、勾股定理、解一元二次方程、三角函数等知识;本题难度较大,综合性强,特别是(2)(3)中,需要运用(1)的结果、勾股定理、三角形面积和分类讨论、三角形全等以及解方程等知识才能得出结果.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
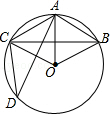 如图,在半径为6cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BC}$上一点,且∠D=30°.
如图,在半径为6cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BC}$上一点,且∠D=30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
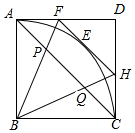 如图,正方形ABCD的边长为$\sqrt{2}$,点E是弧AC上的一个动点,过点E的切线与AD交于点F,与CD交于点H.
如图,正方形ABCD的边长为$\sqrt{2}$,点E是弧AC上的一个动点,过点E的切线与AD交于点F,与CD交于点H. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com