
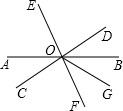
 如图所示,直线AB、CD、EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=64°,求∠AOF、∠DOG的度数.
如图所示,直线AB、CD、EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=64°,求∠AOF、∠DOG的度数. 分析 根据垂线的定义,可得∠COE=∠COF,根据角的和差,可得∠AOF,根据对顶角的性质,可得∠BOF=∠AOE,∠DOB=∠AOC,根据角的和差,可得答案.
解答 解:∵CD⊥EF,得
∠COE=∠COF=90°.
由角的和差,得
∠AOC=∠COE=90°-64°=26°,
∠AOF=∠AOC+∠COF=26°+90°=116°;
由对顶角相等,得
∠BOF=∠AOE=64°,∠DOB=∠AOC=26°,
由OG平分∠BOF,得
∠BOG=$\frac{1}{2}$∠BOF=32°,
由角的和差,得
∠DOG=∠DOB+∠BOG=32°+26°=58°.
点评 本题考查了垂线、角平分线的定义、角的和差,利用垂线的定义、角的和差、对顶角的性质是解题关键.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{7}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{11}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,长方体的长、宽、高分别为5cm、3cm、2cm,一只蚂蚁欲从长方体底面上的点A沿着长方体表面爬到点B处,则蚂蚁需要爬行的最短路程的长为5$\sqrt{2}$cm.
如图,长方体的长、宽、高分别为5cm、3cm、2cm,一只蚂蚁欲从长方体底面上的点A沿着长方体表面爬到点B处,则蚂蚁需要爬行的最短路程的长为5$\sqrt{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com