
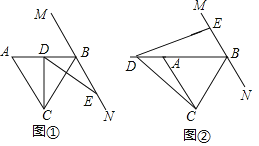
����Ŀ����ͼ����ABC�ǵȱ������Σ�����B��MN��AC��D������BA�ϵĶ��㣬����DC�Ƶ�D��ʱ����ת60��������DE��DE��MN��E��
��1����ͼ������DΪAB�е�ʱ����֤��BD+BE��BC��
��2����ͼ������D��BA�ӳ�����ʱ����1���Ľ����Ƿ����������������֤����������������д��BC��BD��BE�����߶ε�������ϵ����˵�����ɣ�
��3������DCA��15��ʱ��ֱ��д��BD��BE��������ϵ��
���𰸡���1������������2�����۲�������BD��BE��BC������������3��BD����1+![]() ��BE��BD����
��BE��BD����![]() +
+![]() ��BE
��BE
��������
��1����ͼ1�У�����EC������֤��C��D��B��E�ĵ㹲Բ���Ƴ���DCE�ǵȱ������Σ���֤����ACD�ա�BCE��SAS���ɵý��ۣ�
��2����ͼ2�У����۲�������BD��BE��BC��֤���������ƣ�1��������ȫ�������ε����ʽ�����⼴�ɣ�
��3�����������Σ�����ͼ����1�У�����D���߶�AB��ʱ�����ۣ�BD����1+![]() ��BE������ͼ����2�У�����D��BA���ӳ�����ʱ�����ۣ�BD����
��BE������ͼ����2�У�����D��BA���ӳ�����ʱ�����ۣ�BD����![]() +
+![]() ��BE�����ò�����ֱ�������ν�����⼴�ɣ�
��BE�����ò�����ֱ�������ν�����⼴�ɣ�
��1��֤������ͼ1�У�����EC��

�ߡ�ABC�ǵȱ������Σ�
��CA��CB��AB����ACB����ABC��60����
��MN��AC��
���CBE����ACB��60����
�ߡ�CDE��60����
���CDE����CBE��60����
��C��D��B��E�ĵ㹲Բ��
���CED����CBD��60����
���DCE�ǵȱ������Σ�
���ACB����DCE��60����
���ACD����BCE��
���ACD�ա�BCE��SAS����
��AD��BE��
��BC��AB��AD+BD��
��BC��BE+BD��
��2���⣺��ͼ2�У����۲�������BD��BE��BC��
���ɣ�����EC��
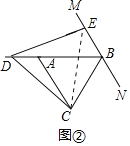
�ߡ�ABC�ǵȱ������Σ�
��CA��CB��AB����ACB����ABC����CAB��60����
��MN��AC��
���EBA����CAB��60����
���EBC��120����
�ߡ�CDE��60����
���CDE+��CBE��180����
��C��D��E��B�ĵ㹲Բ��
���CED����CBD��60����
���DCE�ǵȱ������Σ�
���DCE����ACB��60����
���ACD����BCE��
���ACD�ա�BCE��SAS����
��AD��BE��
��BC��AB��BD��AD
��BC��BD��BE��
��3���⣺����ͼ����1�У�����D���߶�AB��ʱ�����ۣ�BD����1+![]() ��BE��
��BE��
���ɣ���BH��DE��H����DE��ȡһ��K��ʹ��DK��BK������BK��
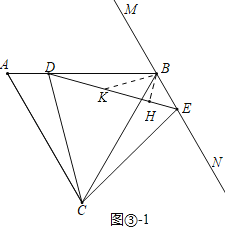
�ߡ�ACD��15������A����CDE��60������BDC����A+��ACD��
���BDE����ACD��60����
��MN��AC��
���CBN����ACB��60����
�ߡ�ABC��60����
���DBE��120������DEB��45����
��BH��DE��
���BHE����BHD��90����
���HBE����HEB��45����
��BH��EH����BH��EH��x����BE��![]() =
=![]() x��
x��
��DK��KB��
���KDB����KBD��15����
���BKE����KDB+��KBD��30����
��BK��DK��2x��KH��BKcos30��=![]() x��
x��
��BD��![]() ��
��![]() ����
����![]() ��x��
��x��
��![]() ��
��![]() ��1+
��1+![]() ��
��
��BD����1+![]() ��BE��
��BE��
����ͼ����2�У�����D��BA���ӳ�����ʱ�����ۣ�BD����![]() +
+![]() ��BE��
��BE��
���ɣ���EH��AB��H��
��DB��ȡһ��G��ʹ��DG��EG������EG��
��EH��m��
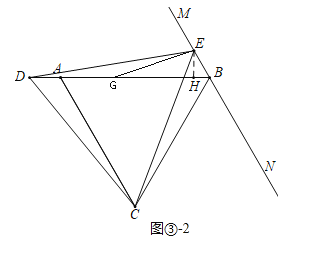
ͬ����֤����EDB��15������EBH��60����
���EGB��30����
����DH��DG+GH=EG+GH=EH��sin30��+EH��tan30��=2m+![]() m��EB=EH��sin60����
m��EB=EH��sin60����![]() m��
m��
��![]() ��
��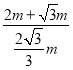 ��
��![]() +
+![]()
��BD����![]() +
+![]() ��BE��
��BE��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��һ����һ���������棬��������һ�µ��������ڹµ�P���ۿ�С����ְ��ں��л�������ͼ��ʾ����С����P���������ر�ƫ��60��������200��A�������������Ϸ�����һ��ʱ�䵽B������B��С���۲�������ڵ�P���ڱ�ƫ��37���ķ����ϣ���ʱС���������������ף���ȷ��1�ף���
���ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75��![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
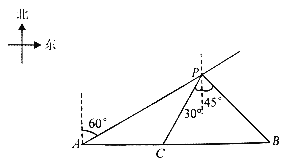
����Ŀ�����գ�������ĸɽ������Ϊ���½����죬��Ϊ�ҹ������ͽ���ĵ�һ�����������ϵĹ�����ĸ������������̫�����Σ���ʹ�ҹ���ΰ����·�ϼ���ǰ����ͼ��ɽ������һ�β����У�Ѳ��������A��ƫ��60�㷽��P���������ں���A����������һ���ɴ�ֻB����BA������ʻ��ɽ�����������ó������ɴ�ֻ��P����ƫ��45�㷽��P��![]() ���ɽ����������P����ƫ��30�㷽��ʻ�����պ���C���ɹ����ؿ��ɴ�ֻ��������ʱ�����ɴ�ֻ�ຣ��A���ж��ٺ����
���ɽ����������P����ƫ��30�㷽��ʻ�����պ���C���ɹ����ؿ��ɴ�ֻ��������ʱ�����ɴ�ֻ�ຣ��A���ж��ٺ����![]() �������ȷ��0.1���
�������ȷ��0.1���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������У��кܶຯ������һ�����ڽ���ʽ�����������ĺ��������ǿ���ͨ���б���ͼ�����������ܴ��ڵ����ʽ���̽����������������һ�����⣺
��֪y��x�ĺ������±���y��x�ļ����Ӧֵ��
x | �� | ��5 | ��4 | ��3 | ��2 | 0 | 1 | 2 | 3 | 4 | 5 | �� |
y | �� | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ��2 | ��1.5 | 0 | 2.5 | �� |
С��ͬѧ����ѧϰ�����ľ��飬������������ӳ����y��x֮��ı仯���ɣ��Ըú�����ͼ�������ʽ�����̽����
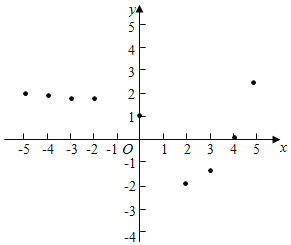
������С��ͬѧ��̽�����̣��벹��������
��1����ͼ����ƽ��֮������ϵxOy�У���������ϱ��и���ӦֵΪ����ĵ㣬��������ĵ㣬����������ͼ��
��2�����ݻ����ĺ���ͼ��ش�
��x����1ʱ����Ӧ�ĺ���ֵy��Ϊ�� ����
��������ֵy��0����x��ȡֵ��Χ���� ����
��д���ú�����һ�����ʣ�������ǰ�����е��ظ������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ᾭ�õķ�չ������������ƽ�����ռң�ij��ѧ��ȤС�������ȡ������ij��λ����ְ�����е��飬��ְ�����������4�ࣨA������40��Ԫ���ϣ�B��������20��40��Ԫ��C��������20��Ԫ���£�D����ʱδ������������ͳ�ƣ�����ͳ�ƽ�����Ƴ���������ͳ��ͼ������ͳ��ͼ������ͼ����Ϣ����������⣺

��1��������������Ϊ�� ����������B�������ٷֱ����� ��������������ͳ��ͼ�е�Բ�ĽǶ������� ����
��2��������ͳ��ͼ����������
��3���õ�λ�ס�������������δ���������ֱ�Ϊ2�˺�3�ˣ��ִ���5������ѡ2��ȥ�ι۳�չ�����б�����״ͼ�ķ�������ѡ����2�����Բ�ͬ���ҵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������10m�ߵĴ���A����ˮ��������ˮ�������ˮ��������״�����������ڵ�ƽ����ǽ�洹ֱ������ͼ��ʾ����������ߵ���ߵ�M��ǽ1m�������![]() m����ˮ����ص�B��ǽ�ľ���OB�ǣ� ��
m����ˮ����ص�B��ǽ�ľ���OB�ǣ� ��
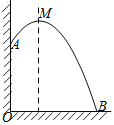
A.2mB.3mC.4mD.5m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ������ҵ��ʱ�������һ�����꾭Ӫ,����һ�ֳɱ�Ϊ30Ԫ/�����Ļ���,�������������۾���,�������������Ļ������ۼ�y1(Ԫ/��),����y2(��)���x(1��x<90)��ĺ���ͼ����ͼ��ʾ(��������=(�ۼ�-�ɱ�)������).
(1)��y1��y2�ĺ�������ʽ.
(2)��ÿ�����������W��x�ĺ�������ʽ.
(3)���������Ļ����ĵڶ�����,�����������,��������Ƕ���?


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��С�ռң��˵أ�������ͬһ��ֱ���ϣ�С�մӼ�ȥ�˵ؽ�ˮ����ȥ������ݣ�Ȼ��ؼң���ͼ��ӳ����������У�С����ҵľ���y��ʱ��x֮��Ķ�Ӧ��ϵ������˵غ͵���ľ���Ϊakm��С���ڵ�����ݱ��ڲ˵ؽ�ˮ������bmin����a��b��ֵ�ֱ�Ϊ��������
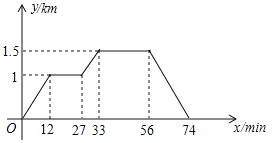
A.1��8B.0.5��12C.1��12D.0.5��8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���![]() �У���
����![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ��һ��
��һ��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��

��1����![]() ��
��![]() ����
����![]() �ij���
�ij���
��2����![]() ����֤��
����֤��![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com