
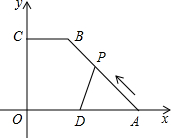
 已知,如图,在直角梯形COAB中,CB∥OA,以O为原点建立平面直角坐标系,A、B、C的坐标分别为A(10,0)、B(4,8)、C(0,8),D为OA的中点,动点P自A点出发沿A→B→C→O的路线移动,速度为每秒1个单位,移动时间记为t秒,
已知,如图,在直角梯形COAB中,CB∥OA,以O为原点建立平面直角坐标系,A、B、C的坐标分别为A(10,0)、B(4,8)、C(0,8),D为OA的中点,动点P自A点出发沿A→B→C→O的路线移动,速度为每秒1个单位,移动时间记为t秒,分析 (1)如图作BE⊥OA于E,作OF⊥AB于F,DH⊥AB于H,得到OE=BC=4,在Rt△ABE中,AE=OA-OE=6,BE=OC=8,求出AB=10,因为OA•BE=AB•OF,得到OF=$\frac{OA•BE}{AB}$=8,DH=$\frac{1}{2}$OF=4,得到S=$\frac{1}{2}AP$•DH=$\frac{1}{2}$t•4=2t,求得t=10时,S最大=20;
(2)本题分两种情况:
①当点P在AB上时,设点P的坐标为(x,y),由S△APD=$\frac{1}{4}$S梯形COAB,得到$\frac{1}{2}$OD•y=$\frac{1}{4}$×56故可求出y的值,由S△APD=$\frac{1}{2}$AP•DH=$\frac{1}{2}$t•4=14,求出t的值,作BG⊥OA于G,由勾股定理即可得出x的值,进而得出点P的坐标;
②当点P在OC上时,设点P的坐标为(0,y).由S△APD═$\frac{1}{4}$S梯形COAB,得到$\frac{1}{2}$OD•y=$\frac{1}{4}$×56故可求出y的值,此时t=10+4+(8-$\frac{28}{5}$)=16$\frac{2}{5}$由此可得出点P的坐标.
解答 解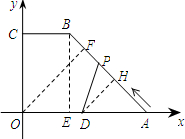 :如图(1)作BE⊥OA于E,作OF⊥AB于F,DH⊥AB于H,OE=BC=4,
:如图(1)作BE⊥OA于E,作OF⊥AB于F,DH⊥AB于H,OE=BC=4,
∵在Rt△ABE中,AE=OA-OE=6,BE=OC=8,
∴AB=10,
∵OA•BE=AB•OF,
∴OF=$\frac{OA•BE}{AB}$=8,DH=$\frac{1}{2}$OF=4,
∴S=$\frac{1}{2}AP$•DH=$\frac{1}{2}$t•4=2t,(0≤t≤10),
当t=10时,S最大=20;
(2)点P只能在AB或OC上才能满足题意,
S梯形COAB=$\frac{1}{2}$(BC+OA)•OC=$\frac{1}{2}$(4+10)×8=56,
①当点P在AB上时,设点P的坐标为(x,y),
∵S△APD=$\frac{1}{4}$S梯形COAB=$\frac{1}{2}$OD•y=$\frac{1}{4}$×56,
∴y=$\frac{28}{5}$,∵S△APD=$\frac{1}{2}$AP•DH=$\frac{1}{2}$t•4=14,
∴t=7,
作BG⊥OA于G,由勾股定理得(AO-x)2+y2=AP2,即即(10-x)2+${(\frac{28}{5})}^{2}$=72,
∴x=$\frac{29}{2}$,∴t=7时,P($\frac{29}{5}$,$\frac{28}{5}$),
②当点P在OC上时,设点P的坐标为(0,y),
∵S△APD=$\frac{1}{4}$S梯形COAB=$\frac{1}{2}$OD•y=$\frac{1}{4}$×56,
∴y=$\frac{28}{5}$,
∴此时t=10+4+(8-$\frac{28}{5}$)=16$\frac{2}{5}$,
∴t=16$\frac{2}{5}$时,P(0,$\frac{28}{5}$),
综上所述:当t=7时,点P($\frac{29}{5}$,$\frac{28}{5}$)或t=16$\frac{2}{5}$时P(0,$\frac{28}{5}$).
点评 本题主要考查了梯形的面积,三角形的面积,勾股定理,最大值,根据题意作出辅助线,构造出三角形及梯形的高是解答此题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com