
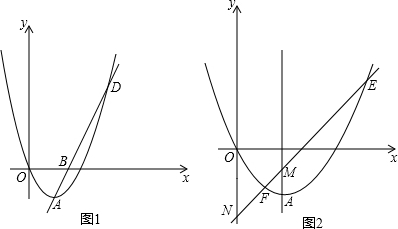
���� ��1������������C1��y=$\frac{1}{2}{x^2}$-2x������ö���A�����꣬��ֱ��AB�Ľ���ʽΪy=kx+b�����ô���ϵ�������ֱ��AB�Ľ���ʽ��Ȼ���������̣��ⷽ���鼴�����D�����ꣻ
��2�����ݴ���ϵ�������ֱ��OD�Ľ���ʽy=x���Ӷ���á�DOK=��ONE=45�㣬��M��2��yM����N��0��yN����E��x1��y1����F��x2��y2�������ݵ���ֱ�������ε����ʵó�NF=$\sqrt{2}$x2��MN=2$\sqrt{2}$��EM=$\sqrt{2}$��x1-2��=$\sqrt{2}$x1-2$\sqrt{2}$����EM-FN=MN�õ�$\sqrt{2}$x1-2$\sqrt{2}$-$\sqrt{2}$x2=2$\sqrt{2}$���Ӷ����x1-x2=4����$\left\{\begin{array}{l}{y=x-m}\\{y=\frac{1}{2}{x}^{2}-2x}\end{array}\right.$��$\frac{1}{2}{x^2}$-3x+m=0�����ݸ���ϵ���Ĺ�ϵ�õ�x1+x2=6��x1x2=2m�������õ���x1-x2��2=��x1+x2��2-4x1x2=16���������õ�62-4��2m=16���ⷽ�����m���ɣ�
��3����G��t��$\frac{1}{2}$t2-2t����ֱ��x=t��x����H��ͨ����OGH�ס�GPH���õ�GH2=OH•PH������$\frac{1}{2}$t2-2t��2=t•PH����������C1��y=$\frac{1}{2}{x^2}$-2x��x���һ������ΪK��4��0�����������ԳƵ����ʵõ�KH=PH=t-4�����ԣ�$\frac{1}{2}$t2-2t��2=t��t-4�����ⷽ�����t���ɣ�
��� 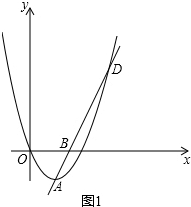 �⣺��1����ͼ1���ߵ�AΪ������C1��y=$\frac{1}{2}{x^2}$-2x�Ķ��㣬
�⣺��1����ͼ1���ߵ�AΪ������C1��y=$\frac{1}{2}{x^2}$-2x�Ķ��㣬
��xA=-$\frac{b}{2a}$=-$\frac{-2}{2��\frac{1}{2}}$=2��
��yA=$\frac{1}{2}$��22-2��2=-2��
��A��2��-2����
�ߵ�B������Ϊ��3��0����
��ֱ��AB�Ľ���ʽΪy=kx+b��
��$\left\{\begin{array}{l}{2k+b=-2}\\{3k+b=0}\end{array}\right.$�����$\left\{\begin{array}{l}{k=2}\\{b=-6}\end{array}\right.$��
��ֱ��AB�Ľ���ʽΪy=2x-6��
��$\left\{\begin{array}{l}{y=2x-6}\\{y=\frac{1}{2}{x}^{2}-2x}\end{array}\right.$��$\left\{\begin{array}{l}{x=6}\\{y=6}\end{array}\right.$��$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$��
���D��������6��6����
��2����ͼ2����ֱ��OD�Ľ���ʽΪy=ax��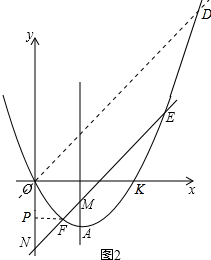
��6=6a�����a=1��
��ֱ��OD�Ľ���ʽΪy=x��
��D�ĺ�����������궼����6��
���DOK=45�㣬
��EF��OD��
���ONE=45�㣬
��M��2��yM����N��0��yN����E��x1��y1����F��x2��y2����
��F��FP��y����P��
��NF=$\sqrt{2}$x2��
ͬ����MN=2$\sqrt{2}$��EM=$\sqrt{2}$��x1-2��=$\sqrt{2}$x1-2$\sqrt{2}$��
��EM-FN=MN��
��$\sqrt{2}$x1-2$\sqrt{2}$-$\sqrt{2}$x2=2$\sqrt{2}$��
��x1-x2=4��
��ֱ��EF�Ľ���ʽΪy=x-m��
��$\left\{\begin{array}{l}{y=x-m}\\{y=\frac{1}{2}{x}^{2}-2x}\end{array}\right.$��$\frac{1}{2}{x^2}$-3x+m=0��
��x1+x2=-$\frac{b}{a}$=-$\frac{-3}{\frac{1}{2}}$=6��x1x2=$\frac{c}{a}$=2m��
�ࣨx1-x2��2=��x1+x2��2-4x1x2=16��
��62-4��2m=16�����m=$\frac{5}{2}$��
��3����ͼ3����G��t��$\frac{1}{2}$t2-2t����ֱ��x=t��x����H��
��GP��GO��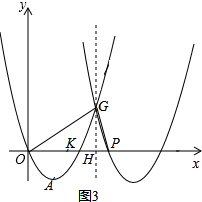
���OGP=90�㣬
�ߡ�OGH+��HGP=��OGH+��GOH=90�㣬
���HGP=��GOH��
���OGH�ס�GPH��
��GH2=OH•PH������$\frac{1}{2}$t2-2t��2=t•PH��
��������C1��y=$\frac{1}{2}{x^2}$-2x��x���һ������ΪK��4��0����
��KH=PH=t-4��
��PH=t-4��
�ࣨ$\frac{1}{2}$t2-2t��2=t��t-4����
��$\frac{1}{2}$t2-2t��0��
��t1=2+2$\sqrt{2}$��t2=2-2$\sqrt{2}$��
��t=2��2$\sqrt{2}$��
���� ���⿼���˴���ϵ������һ�κ����Ľ���ʽ������ֱ�������ε����ʣ���������������������Ƶ��ж������ʣ��ⷽ�̺ͷ�����ȣ�������������ͼ���ǽ���Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
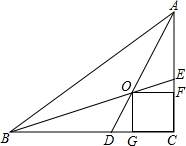 ��ͼ����Rt��ABC�У�����ǵ�ƽ����AD��BE�ཻ�ڵ�O��OF��AC�ڵ�F��OG��BC�ڵ�G����֤���ı���OGCF�������Σ�
��ͼ����Rt��ABC�У�����ǵ�ƽ����AD��BE�ཻ�ڵ�O��OF��AC�ڵ�F��OG��BC�ڵ�G����֤���ı���OGCF�������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
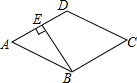 ��ͼ��������ABCD�У���ABC=120�㣬��BE��AD������Ϊ��E����֤��AE=DE��
��ͼ��������ABCD�У���ABC=120�㣬��BE��AD������Ϊ��E����֤��AE=DE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
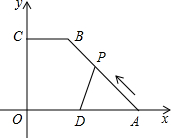 ��֪����ͼ����ֱ������COAB�У�CB��OA����OΪԭ�㽨��ƽ��ֱ������ϵ��A��B��C������ֱ�ΪA��10��0����B��4��8����C��0��8����DΪOA���е㣬����P��A�������A��B��C��O��·���ƶ����ٶ�Ϊÿ��1����λ���ƶ�ʱ���Ϊt�룬
��֪����ͼ����ֱ������COAB�У�CB��OA����OΪԭ�㽨��ƽ��ֱ������ϵ��A��B��C������ֱ�ΪA��10��0����B��4��8����C��0��8����DΪOA���е㣬����P��A�������A��B��C��O��·���ƶ����ٶ�Ϊÿ��1����λ���ƶ�ʱ���Ϊt�룬�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
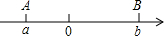 �Ķ�������ϣ���A��B�������Ϸֱ��ʾ������a��b��A��B����֮��ľ����ʾΪAB����������A��B����֮��ľ���AB=|a-b|���ش��������⣺
�Ķ�������ϣ���A��B�������Ϸֱ��ʾ������a��b��A��B����֮��ľ����ʾΪAB����������A��B����֮��ľ���AB=|a-b|���ش��������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com