
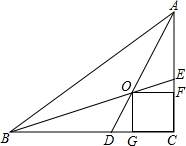
 如图,在Rt△ABC中,两锐角的平分线AD,BE相交于点O,OF⊥AC于点F,OG⊥BC于点G,求证:四边形OGCF是正方形.
如图,在Rt△ABC中,两锐角的平分线AD,BE相交于点O,OF⊥AC于点F,OG⊥BC于点G,求证:四边形OGCF是正方形.  导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:解答题
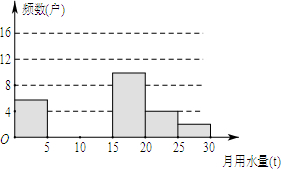 某校社会活动实践小组的同学们为了解2015年教工小区家庭月平均用水情况,随机调查了该小区部分家庭,并将调查数据整理成如下的统计表和直方图
某校社会活动实践小组的同学们为了解2015年教工小区家庭月平均用水情况,随机调查了该小区部分家庭,并将调查数据整理成如下的统计表和直方图| 月平均用水量x(t) | 频数(户) | 频率 |
| 0<x≤5 | 6 | 0.12 |
| 5<x≤10 | m | 0.24 |
| 10<x≤15 | n | 0.32 |
| 15<x≤20 | 10 | 0.20 |
| 20<x≤25 | 4 | k |
| 25<x≤30 | 2 | 0.04 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com