
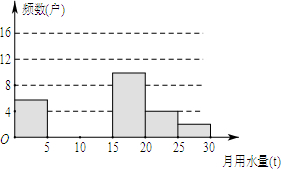
 ijУ���ʵ��С���ͬѧ��Ϊ�˽�2015��̹�С����ͥ��ƽ����ˮ�������������˸�С�����ּ�ͥ�����������������������µ�ͳ�Ʊ���ֱ��ͼ
ijУ���ʵ��С���ͬѧ��Ϊ�˽�2015��̹�С����ͥ��ƽ����ˮ�������������˸�С�����ּ�ͥ�����������������������µ�ͳ�Ʊ���ֱ��ͼ| ��ƽ����ˮ��x��t�� | Ƶ�������� | Ƶ�� |
| 0��x��5 | 6 | 0.12 |
| 5��x��10 | m | 0.24 |
| 10��x��15 | n | 0.32 |
| 15��x��20 | 10 | 0.20 |
| 20��x��25 | 4 | k |
| 25��x��30 | 2 | 0.04 |
���� ��1�����ݵ�һ���Ƶ����6����Ӧ��Ƶ����0.12���ݴ˼�����õ������������Ȼ�����Ƶ�ʵ��������m��n��ֵ��
��2�����ݣ�1���Ľ�����ɲ�ȫֱ��ͼ��
��3����������1500���Զ�Ӧ�İٷֱȼ�����ã�
��� �⣺��1��������������ǣ�6��0.12=50��������
��m=50��0.24=12��n=50��0.32=16��������
��2����ͼ��ʾ��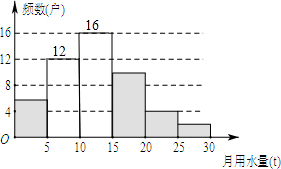 ��
��
��3��1500��1-0.12-0.24-0.32-0.20��=180��������
�𣺹��Ƹ�С����ƽ����ˮ������20t�ļ�ͥ��Լ��180����
���� ���⿼���Ƶ���ֲ�ֱ��ͼ������������ͳ��ͼ��ȡ��Ϣ������������ͳ��ͼ��ȡ��Ϣʱ����������۲졢�������о�ͳ��ͼ������������ȷ���жϺͽ�����⣮


 ��Уͨ��֤��Ч��ҵϵ�д�
��Уͨ��֤��Ч��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2+a2=2a4 | B�� | ��1-a����1+a��=a2-1 | C�� | ��-3a2b��3=-9a6b3 | D�� | 3a��-2a��3=-24a4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2a+3b=5ab | B�� | ��3a3��2=6a6 | C�� | a6+a2=a3 | D�� | -3a+2a=-a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ƽ���ı��� | B�� | ���� | C�� | ���� | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
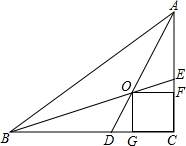 ��ͼ����Rt��ABC�У�����ǵ�ƽ����AD��BE�ཻ�ڵ�O��OF��AC�ڵ�F��OG��BC�ڵ�G����֤���ı���OGCF�������Σ�
��ͼ����Rt��ABC�У�����ǵ�ƽ����AD��BE�ཻ�ڵ�O��OF��AC�ڵ�F��OG��BC�ڵ�G����֤���ı���OGCF�������Σ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com