
分析 先分母有理化,然后根据二次根式的加减运算法则进行计算.
解答 解:原式=$\frac{(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$+$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$+$\frac{\sqrt{4}-\sqrt{3}}{(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})}$+…+$\frac{\sqrt{2012}-\sqrt{2011}}{(\sqrt{2012}+\sqrt{2011})(\sqrt{2012}-\sqrt{2011})}$+$\frac{\sqrt{2013}-\sqrt{2012}}{(\sqrt{2013}+\sqrt{2012})(\sqrt{2013}-\sqrt{2012})}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2012}$-$\sqrt{2011}$+$\sqrt{2013}$-$\sqrt{2012}$
=-1+$\sqrt{2013}$.
点评 主要考查二次根式的有理化.根据二次根式的乘除法法则进行二次根式有理化.二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | -x2+3x2=2 | B. | x2×x3=x6 | ||
| C. | (x+1)(-x-1)=-x2-2x-1 | D. | $\frac{{x}^{2}-4}{x-2}$=x-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
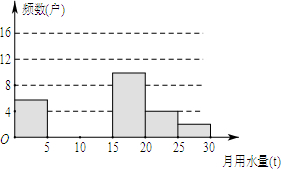 某校社会活动实践小组的同学们为了解2015年教工小区家庭月平均用水情况,随机调查了该小区部分家庭,并将调查数据整理成如下的统计表和直方图
某校社会活动实践小组的同学们为了解2015年教工小区家庭月平均用水情况,随机调查了该小区部分家庭,并将调查数据整理成如下的统计表和直方图| 月平均用水量x(t) | 频数(户) | 频率 |
| 0<x≤5 | 6 | 0.12 |
| 5<x≤10 | m | 0.24 |
| 10<x≤15 | n | 0.32 |
| 15<x≤20 | 10 | 0.20 |
| 20<x≤25 | 4 | k |
| 25<x≤30 | 2 | 0.04 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com