
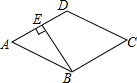
 如图,在菱形ABCD中,∠ABC=120°,作BE⊥AD,垂足为点E,求证:AE=DE.
如图,在菱形ABCD中,∠ABC=120°,作BE⊥AD,垂足为点E,求证:AE=DE. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某校有一块长为(3a+2b)米,宽为(2a+3b)米的长方形地块,规划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当a=4,b=3时的绿化面积.
如图,某校有一块长为(3a+2b)米,宽为(2a+3b)米的长方形地块,规划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当a=4,b=3时的绿化面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 天水历史悠久,文物古迹星罗棋布,是中国历史文化名城,也是中国优秀旅游城市.如图是秦州区的部分旅游景点,请你以中心广场为坐标原点建立坐标系,并写出各景点的坐标:
天水历史悠久,文物古迹星罗棋布,是中国历史文化名城,也是中国优秀旅游城市.如图是秦州区的部分旅游景点,请你以中心广场为坐标原点建立坐标系,并写出各景点的坐标:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
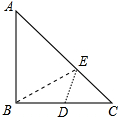 如图,在Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值是( )
如图,在Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值是( )| A. | $2\sqrt{5}+2$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{5}$ | D. | $2\sqrt{3}+2$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com