
分析 首先将分式进行约分化简,可得$\frac{6}{3-a}$,要使分式的值为正整数,那么3-a只能取6的正整数约数1,2,3,6,这样就可以求得相应a的值.
解答 解:$-\frac{6(a+3)}{{a}^{2}-9}=-\frac{6(a+3)}{(a+3)(a-3)}=\frac{6}{3-a}$,
由分式$-\frac{6(a+3)}{{a}^{2}-9}$的值为正整数,可知3-a为6的正整数约数,
故3-a=1,2,3,6,
由3-a=1,得a=2,
由3-a=2,得a=1,
由3-a=3,得a=0,
由3-a=6,得a=-3,
而当a=-3时,a2-9=0,分式无意义,故a=-3舍去,
所以a的值为2或1或0.
点评 本题考查了分式的化简求值问题,解题时要注意分式有意义的条件,即分式的分母不能为0.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
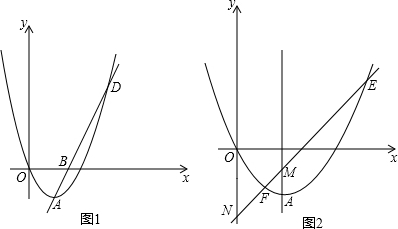
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
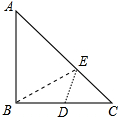 如图,在Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值是( )
如图,在Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值是( )| A. | $2\sqrt{5}+2$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{5}$ | D. | $2\sqrt{3}+2$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
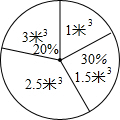 为了宣传保护水源、节约用水的生活方式,某同学利用课余时间对某小区居民的用水情况进行了统计,并将今年1月居民的节水量统计整理成如下统计图表:
为了宣传保护水源、节约用水的生活方式,某同学利用课余时间对某小区居民的用水情况进行了统计,并将今年1月居民的节水量统计整理成如下统计图表:| 节水量(米3) | 1 | 1.5 | 2.5 | 3 |
| 户数 | a | 90 | 100 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
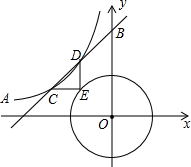 如图,直线y=x+3$\sqrt{2}$与反比例函数y=$\frac{k}{x}$的图象交于C、D两点,⊙O是以CD长为半径的圆,CE∥x轴,DE∥y轴,求k的值.
如图,直线y=x+3$\sqrt{2}$与反比例函数y=$\frac{k}{x}$的图象交于C、D两点,⊙O是以CD长为半径的圆,CE∥x轴,DE∥y轴,求k的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com