
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
(1) ①直接写出抛物线的对称轴是________;
②用含a的代数式表示b;
(2)横、纵坐标都是整数的点叫整点.点A恰好为整点,若抛物线在点A,B之间的部分与线段AB所围成的区域内(不含边界)恰有1个整点,结合函数的图象,直接写出a的取值范围.
【答案】(1)①直线x=1;②b=-2a;(2)-2≤a<-1或1<a≤2.
【解析】
(1) ①根据抛物线的对称性可以直接得出其对称轴;②利用对称轴公式![]() 进一步求解即可;
进一步求解即可;
(2)分两种情况:①![]() ,②
,②![]() ,据此依次讨论即可.
,据此依次讨论即可.
解:(1)①∵当x=0时,y=c,∴点A坐标为(0,c),
∵点A向右平移2个单位长度,得到点B,∴点B(2,c),
∵点B在抛物线上,∴抛物线的对称轴是:直线x=1;
故答案为:直线x=1;
②∵抛物线的对称轴是直线:x=1,∴![]() ,即
,即![]() ;
;
(2)①如图,若![]() ,
,

因为点A(0,c),B(2,c)都是整点,且指定区域内恰有一个整点,因此这个整点D的坐标必为(1,c-1),但是从运算层面如何保证“恰有一个”呢,与抛物线的顶点C(1,c-a)做位置与数量关系上的比较,必须考虑到紧邻点D的另一个整点E(1,c-2)不在指定区域内,所以可列出不等式组:
![]() ,解得:
,解得:![]() ;
;
②如图,若![]() ,
,
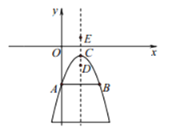
同理可得:![]() ,解得:
,解得:![]() ;
;
综上所述,符合题意的a的取值范围是-2≤a<-1或1<a≤2.


科目:初中数学 来源: 题型:
【题目】如图所示,直线y=![]() x+2与双曲线y=
x+2与双曲线y=![]() 相交于点A(2,n),与x轴交于点C.
相交于点A(2,n),与x轴交于点C.
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为5,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店分两次购进A、B两种商品进行销售,每次购进同一种商品的进价相同,具体情况如下表所示:
(1)求A、B两种商品每件的进价分别是多少元?
(2)商店计划用5300元的资金进行第三次进货,共进A、B两种商品100件,其中要求B商品的数量不少于A商品的数量,有几种进货方案?
(3)综合考虑(2)的情况,商店计划对第三次购进的100件商品全部销售,A商品售价为30元/件,每销售一件A商品需捐款a元(1≤a≤10)给希望工程,B商品售价为100元/件,每销售一件B商品需捐款b元给希望工程,a+b=14.直接写出当b= 时,销售利润最大,最大利润为 元.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想要测量一棵树DE的高度,他在A处测得树顶端E的仰角为30°,他走下台阶到达C处,测得树的顶端E的仰角是60°.已知A点离地面的高度AB=2米,∠BCA=30°,且B,C,D三点在同一直线上.求树DE的高度;
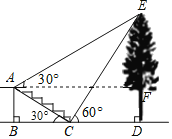
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过圆外一点作这个圆的两条切线”的尺规作图过程.
已知:⊙O及⊙O外一点P.
求作:直线PA和直线PB,使PA切⊙O于点A,PB切⊙O于点B.
作法:如图,
①连接OP,分别以点O和点P为圆心,大于![]() OP的同样长为半径作弧,两弧分别交于点M,N;
OP的同样长为半径作弧,两弧分别交于点M,N;
②连接MN,交OP于点Q,再以点Q为圆心,OQ的长为半径作弧,交⊙O于点A和点B;
③作直线PA和直线PB.
所以直线PA和PB就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
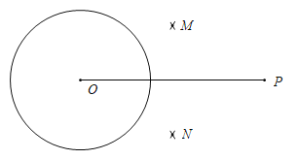
(2)完成下面的证明.
证明:∵OP是⊙Q的直径,
∴ ∠OAP=∠OBP=________°( )(填推理的依据).
∴PA⊥OA,PB⊥OB.
∵OA,OB为⊙O的半径,
∴PA,PB是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京市第十五届人大常委会第十六次会议表决通过《关于修改<北京市生活垃圾管理条例>的决定》,规定将生活垃圾分为厨余垃圾、可回收物、有害垃圾、其它垃圾四大基本品类,修改后的条例将于2020年5月1日实施 .某小区决定在2020年1月到3月期间在小区内设置四种垃圾分类厢:厨余垃圾、可回收物、有害垃圾、其它垃圾,分别记为A、B、C、D,进行垃圾分类试投放,以增强居民垃圾分类意识.
(1)小明家按要求将自家的生活垃圾分成了四类,小明从分好类的垃圾中随机拿了一袋,并随机投入一个垃圾箱中,请用画树状图的方法求垃圾投放正确的概率;
(2)为调查居民生活垃圾分类投放情况,现随机抽取了该小区四类垃圾箱中共1 000千克生活垃圾,数据统计如下(单位:千克):
A | B | C | D | |
厨余垃圾 | 400 | 100 | 40 | 60 |
可回收物 | 25 | 140 | 20 | 15 |
有害垃圾 | 5 | 20 | 60 | 15 |
其它垃圾 | 25 | 15 | 20 | 40 |
求“厨余垃圾”投放正确的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,则下列结论:①
的图象如图所示,则下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() :④方程
:④方程![]()
![]() 有两个大于-1的实数根.其中正确的是( )
有两个大于-1的实数根.其中正确的是( )
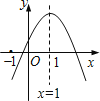
A.①②③B.①②④C.②③④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
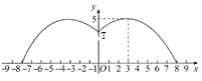
【题目】有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的立杆上点T处汇合.如图所示为截面图,以水平方向为x轴,喷水池中心为原点建立直角坐标系
(1)求水柱所在抛物线(第一象限部分)的函数解析式
(2)正在喷水时,身高1.8米的人,应站在离水池中心多远的地方就能不被淋湿?
(3)在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心的立杆上点T处汇合,请探究扩建后喷水池水柱的最大高度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com