
����Ŀ��ij�̵�����ι���A��B������Ʒ�������ۣ�ÿ�ι���ͬһ����Ʒ�Ľ�����ͬ������������±���ʾ��
��1����A��B������Ʒÿ���Ľ��۷ֱ��Ƕ���Ԫ��
��2���̵�ƻ���5300Ԫ���ʽ���е����ν���������A��B������Ʒ100��������Ҫ��B��Ʒ������������A��Ʒ���������м��ֽ���������
��3���ۺϿ��ǣ�2����������̵�ƻ��Ե����ι�����100����Ʒȫ�����ۣ�A��Ʒ�ۼ�Ϊ30Ԫ/����ÿ����һ��A��Ʒ����aԪ��1��a��10����ϣ�����̣�B��Ʒ�ۼ�Ϊ100Ԫ/����ÿ����һ��B��Ʒ����bԪ��ϣ�����̣�a+b��14��ֱ��д����b���� ��ʱ��������������������Ϊ�� ��Ԫ��

���𰸡���1��ÿ��A��Ʒ�Ľ���Ϊ20Ԫ��ÿ��B��Ʒ�Ľ���Ϊ80Ԫ����2����6�ֽ�����������3��4��880
��������
��1����ÿ��A��Ʒ�Ľ���ΪxԪ��ÿ��B��Ʒ�Ľ���ΪyԪ������ǰ���ν������������ܼۣ����ɵó�����x��y�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
��2���蹺��A��Ʒm������B��Ʒ��100��m��������B��Ʒ������������A��Ʒ���������ܼ۲�����5300Ԫ�����ɵó�����m��һԪһ�β���ʽ�飬��֮���ɵó�m��ȡֵ��Χ�����mΪ�������ɵó�������������
��3����1��a��10��a+b��14�ɵó�4��b��13����������ΪwԪ���������������������������������ɵó�w����b�ĺ�����ϵʽ��������һ�κ��������ʼ��ɽ����ֵ���⣮
��1����ÿ��A��Ʒ�Ľ���ΪxԪ��ÿ��B��Ʒ�Ľ���ΪyԪ��
�����⣬�ã�![]() ��
��
��ã�![]() ��
��
��ÿ��A��Ʒ�Ľ���Ϊ20Ԫ��ÿ��B��Ʒ�Ľ���Ϊ80Ԫ��
��2���蹺��A��Ʒm������B��Ʒ��100��m������
�����⣬�ã�![]() ��
��
��ã�45��m��50��
��m������
��m��ֵ����Ϊ45��46��47��48��49��50��
�6�ֽ���������
��3����1��a��10��a+b��14��
��4��b��13��
��������ΪwԪ��
�����⣬�ã�w��[30��20����14��b��]m+��100��80��b����100��m������2m��100��b��24m+2000��
��2m��100��0��
��w��bֵ�������С��
�൱b��4��m��45ʱ��wȡ�����ֵ�����ֵΪ880��
�ʴ�Ϊ��4��880��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ����ҵ�Ŷ�ץס�̻�������һ���ɹ���װ��Ӫ�����������С��װ����ۣ�ÿ���ɱ�3Ԫ�������ڼ䷢��ÿ���������![]() ����
����![]() �����۵���
�����۵���![]() ��Ԫ
��Ԫ![]() ֮������һ�κ�����ϵ���������������ʾ������3.5��x��5.5������ÿ�컹��֧�������������80Ԫ��
֮������һ�κ�����ϵ���������������ʾ������3.5��x��5.5������ÿ�컹��֧�������������80Ԫ��
���۵��� | 3.5 | 5.5 |
������ | 280 | 120 |
��1�������![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2����ÿ�������Ϊ![]() Ԫ�������۵��۶�Ϊ����Ԫʱ��ÿ������������������Ƕ���Ԫ��
Ԫ�������۵��۶�Ϊ����Ԫʱ��ÿ������������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
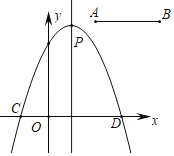
����Ŀ����ͼ���߶�AB��A��2��3����B��5��3����������y������x��1��2��m2+2m+1��x�����������ֱ�ΪC��D����C�ڵ�D����ࣩ
��1����mΪ��ֵʱ�����߹�ԭ�㣬�������ʱ�����ߵĽ���ʽ���Գ����������꣮
��2���������ߵĶ���ΪP��mΪ��ֵʱ��PCD���������������Ƕ��٣�
��3�����߶�AB��y������ƽ��n����λ����m��n�������Ĺ�ϵʱ���������ܰ��߶�AB�ֳ�1��2�����֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ����
��ֱ����![]() ��
��![]() �����ߣ��е�Ϊ
�����ߣ��е�Ϊ![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ���е�.
���е�.
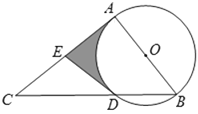
(1)���ж�ֱ��![]() ��
��![]() ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�
(2)��![]() �İ뾶Ϊ2��
�İ뾶Ϊ2��![]() ��
��![]() ����ͼ����Ӱ���ֵ��ܳ�.
����ͼ����Ӱ���ֵ��ܳ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
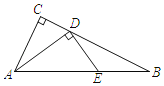
����Ŀ����ͼ��Rt��ABC�У���C��90����DΪBC����һ���㣬��D��DE��AD��AB��E��AC��2��BC��4����D���C���˶���B��ʱ����E�˶���·����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
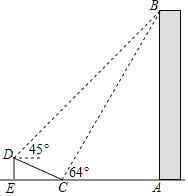
����Ŀ����ͼ���ڴ�¥AB����ǰ����һб��CD��CD=13�ף��±�DE:EC=1�� ![]() ����ΪDE����б���µĵ�C�����¥��B������Ϊ64������б���ϵĵ�D�����¥��B������Ϊ45��������A��C��E��ͬһֱ���ϣ�
����ΪDE����б���µĵ�C�����¥��B������Ϊ64������б���ϵĵ�D�����¥��B������Ϊ45��������A��C��E��ͬһֱ���ϣ�
��1����б��CD�ĸ߶�DE��
��2�����¥AB�ĸ߶ȣ����ο����ݣ�sin64���0.9��tan64���2����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������·���������ABC��������С��ԭ����![]() ����ͼ����ȡһ��O����AO��BO��CO����ȡ���ǵ��е�D��E��F������DEF��������˵����ȷ�ĸ����ǣ�������
����ͼ����ȡһ��O����AO��BO��CO����ȡ���ǵ��е�D��E��F������DEF��������˵����ȷ�ĸ����ǣ�������
����ABC����DEF��λ��ͼ������ABC����DEF������ͼ��
����ABC����DEF���ܳ���Ϊ1��2����ABC����DEF�������Ϊ4��1��
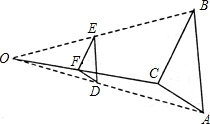
A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�������
��������![]() ��
��![]() �ύ�ڵ�A������A����ƽ��2����λ���ȣ��õ���B����B���������ϣ�
�ύ�ڵ�A������A����ƽ��2����λ���ȣ��õ���B����B���������ϣ�
��1�� ��ֱ��д�������ߵĶԳ�����________��
���ú�a�Ĵ���ʽ��ʾb��
��2���ᡢ�����궼�������ĵ�����㣮��Aǡ��Ϊ���㣬���������ڵ�A��B֮��IJ������߶�AB��Χ�ɵ������ڣ������߽磩ǡ��1�����㣬��Ϻ�����ͼ��ֱ��д��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڷ���������![]() ������˵������ȷ���ǣ�������
������˵������ȷ���ǣ�������
A. ����ͼ��ֱ�λ�ڵ�һ����������
B. ��x��0ʱ��y��x���������С
C. ����A��x1��y1����B��x2��y2�����ں���ͼ���ϣ���x1��x2����y1��y2
D. ����ͼ���㣨1��2��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com