
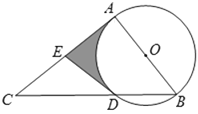
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的切线,切点为
的切线,切点为![]() ,
,![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
(1)试判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若![]() 的半径为2,
的半径为2,![]() ,
,![]() ,求图中阴影部分的周长.
,求图中阴影部分的周长.
【答案】(1)直线![]() 与
与![]() 相切;理由见解析;(2)
相切;理由见解析;(2)![]() .
.
【解析】
(1)连接OE、OD,根据切线的性质得到∠OAC=90°,根据三角形中位线定理得到OE∥BC,证明△AOE≌△DOE,根据全等三角形的性质、切线的判定定理证明;
(2)根据切线长定理可得DE=AE=2.5,由圆周角定理可得∠AOD=100°,然后根据弧长公式计算弧AD的长,从而可求得结论.
解:(1)直线DE与⊙O相切,
理由如下:连接OE、OD,如图,
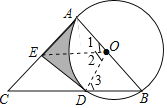
∵AC是⊙O的切线,
∴AB⊥AC,
∴∠OAC=90°,
∵点E是AC的中点,O点为AB的中点,
∴OE∥BC,
∴∠1=∠B,∠2=∠3,
∵OB=OD,
∴∠B=∠3,
∴∠1=∠2,
在△AOE和△DOE中
∵OA=OD
∠1=∠2
OE=OE,
∴△AOE≌△DOE(SAS)
∴∠ODE=∠OAE=90°,
∴DE⊥OD,
∵OD为⊙O的半径,
∴DE为⊙O的切线;
(2)∵DE、AE是⊙O的切线,
∴DE=AE,
∵点E是AC的中点,
∴DE=AE=![]() AC=2.5,
AC=2.5,
∵∠AOD=2∠B=2×50°=100°,
∴阴影部分的周长=![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】已知:抛物线![]()
![]() .
.
(1)求证:抛物线与![]() 轴有两个交点.
轴有两个交点.
(2)设抛物线与![]() 轴的两个交点的横坐标分别为
轴的两个交点的横坐标分别为![]() ,
,![]() (其中
(其中![]() ).若
).若![]() 是关于
是关于![]() 的函数、且
的函数、且![]() ,求这个函数的表达式;
,求这个函数的表达式;
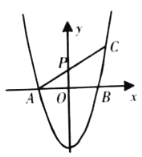
(3)若![]() ,将抛物线向上平移一个单位后与
,将抛物线向上平移一个单位后与![]() 轴交于点
轴交于点![]() 、
、![]() .平移后如图所示,过
.平移后如图所示,过![]() 作直线
作直线![]() ,分别交
,分别交![]() 的正半轴于点
的正半轴于点![]() 和抛物线于点
和抛物线于点![]() ,且
,且![]() .
.![]() 是线段
是线段![]() 上一动点,求
上一动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线y=![]() x+2与双曲线y=
x+2与双曲线y=![]() 相交于点A(2,n),与x轴交于点C.
相交于点A(2,n),与x轴交于点C.
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为5,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017四川省凉山州,第24题,8分)为了推进我州校园篮球运动的发展,2017年四川省中小学生男子篮球赛于2月在西昌成功举办.在此期间,某体育文化用品商店计划一次性购进篮球和排球共60个,其进价与售价间的关系如下表:

(1)商店用4200元购进这批篮球和排球,求购进篮球和排球各多少个?
(2)设商店所获利润为y(单位:元),购进篮球的个数为x(单位:个),请写出y与x之间的函数关系式(不要求写出x的取值范围);
(3)若要使商店的进货成本在4300元的限额内,且全部销售完后所获利润不低于1400元,请你列举出商店所有进货方案,并求出最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个一元二次方程的两个实数根的比值与另一个一元二次方程的两个实数根的比值相等,我们称这两个方程为“相似方程”,例如,![]() 的实数根是3或6,
的实数根是3或6,![]() 的实数根是1或2,
的实数根是1或2,![]() ,则一元二次方程
,则一元二次方程![]() 与
与![]() 为相似方程.下列各组方程不是相似方程的是( )
为相似方程.下列各组方程不是相似方程的是( )
A.![]() 与
与![]() B.
B.![]() 与
与![]()
C.![]() 与
与![]() D.
D.![]() 与
与![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店分两次购进A、B两种商品进行销售,每次购进同一种商品的进价相同,具体情况如下表所示:
(1)求A、B两种商品每件的进价分别是多少元?
(2)商店计划用5300元的资金进行第三次进货,共进A、B两种商品100件,其中要求B商品的数量不少于A商品的数量,有几种进货方案?
(3)综合考虑(2)的情况,商店计划对第三次购进的100件商品全部销售,A商品售价为30元/件,每销售一件A商品需捐款a元(1≤a≤10)给希望工程,B商品售价为100元/件,每销售一件B商品需捐款b元给希望工程,a+b=14.直接写出当b= 时,销售利润最大,最大利润为 元.

查看答案和解析>>
科目:初中数学 来源: 题型:
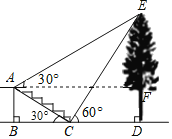
【题目】小明想要测量一棵树DE的高度,他在A处测得树顶端E的仰角为30°,他走下台阶到达C处,测得树的顶端E的仰角是60°.已知A点离地面的高度AB=2米,∠BCA=30°,且B,C,D三点在同一直线上.求树DE的高度;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com