
【题目】定义:如果一个一元二次方程的两个实数根的比值与另一个一元二次方程的两个实数根的比值相等,我们称这两个方程为“相似方程”,例如,![]() 的实数根是3或6,
的实数根是3或6,![]() 的实数根是1或2,
的实数根是1或2,![]() ,则一元二次方程
,则一元二次方程![]() 与
与![]() 为相似方程.下列各组方程不是相似方程的是( )
为相似方程.下列各组方程不是相似方程的是( )
A.![]() 与
与![]() B.
B.![]() 与
与![]()
C.![]() 与
与![]() D.
D.![]() 与
与![]()
【答案】C
【解析】
根据“相似方程”的定义逐项分析即可.
A. ∵![]() ,
,
∴![]() .
.
∴x1=4,x2=-4,
∵![]() ,
,
∴x1=5,x2=-5.
∵4:(-4)=5:(5),
∴![]() 与
与![]() 是相似方程,故不符合题意;
是相似方程,故不符合题意;
B. ∵![]() ,
,
∴x1=x2=6.
∵![]() ,
,
∴(x+2)2=0,
∴x1=x2=-2.
∵6:6=(-2):(-2),
∴![]() 与
与![]() 是相似方程,故不符合题意;
是相似方程,故不符合题意;
C. ∵![]() ,
,
∴![]() ,
,
∴x1=0,x2=7.
∵![]() ,
,
∴![]() ,
,
∴(x-2)(x+3)=0,
∴x1=2,x2=-3.
∵0:7≠2:(-3),
∴![]() 与
与![]() 不是相似方程,符合题意;
不是相似方程,符合题意;
D. ∵![]() ,
,
∴x1=-2,x2=-8.
∵![]() ,
,
∴(x-1)(x-4)=0,
∴x1=1,x2=4.
∵(-2):(-8)=1:4,
∴![]() 与
与![]() 是相似方程,故不符合题意;
是相似方程,故不符合题意;
故选C.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于
轴分别相交于![]() 、
、![]() 两点,点
两点,点![]() 是
是![]() 的中点,点
的中点,点![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 上的动点,将
上的动点,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 的对称点
的对称点![]() 恰好落在线段
恰好落在线段![]() 上(不与端点重合).连接
上(不与端点重合).连接![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() .
.
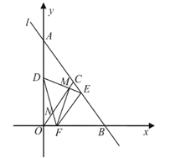
(1)求![]() 的值;
的值;
(2)试判断![]() 与
与![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(3)若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的方程
的方程![]()
(1)求证:无论![]() 为何值,方程总有实数根.
为何值,方程总有实数根.
(2)设![]() ,
,![]() 是方程
是方程![]() 的两个根,记
的两个根,记![]() ,S的值能为2吗?若能,求出此时
,S的值能为2吗?若能,求出此时![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
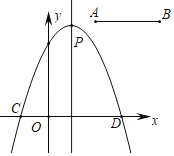
【题目】如图,线段AB,A(2,3),B(5,3),抛物线y=﹣(x﹣1)2﹣m2+2m+1与x轴的两个交点分别为C,D(点C在点D的左侧)
(1)求m为何值时抛物线过原点,并求出此时抛物线的解析式及对称轴和项点坐标.
(2)设抛物线的顶点为P,m为何值时△PCD的面积最大,最大面积是多少.
(3)将线段AB沿y轴向下平移n个单位,求当m与n有怎样的关系时,抛物线能把线段AB分成1:2两部分.
查看答案和解析>>
科目:初中数学 来源: 题型:
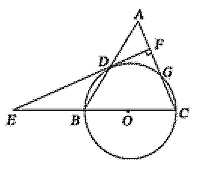
【题目】如图,等腰三角形ABC中,AC=BC=6,AB=8,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
(1)求证:直线EF是⊙O的切线;
(2)求sin∠E的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
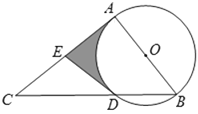
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的切线,切点为
的切线,切点为![]() ,
,![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
(1)试判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若![]() 的半径为2,
的半径为2,![]() ,
,![]() ,求图中阴影部分的周长.
,求图中阴影部分的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
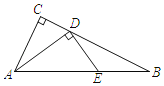
【题目】如图,Rt△ABC中,∠C=90°,D为BC边上一动点,过D作DE⊥AD交AB于E,AC=2,BC=4,当D点从C点运动到B点时,点E运动的路径长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
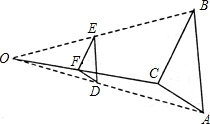
【题目】按如下方法,将△ABC的三边缩小的原来的![]() ,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的个数是( )
,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的个数是( )
①△ABC与△DEF是位似图形②△ABC与△DEF是相似图形
③△ABC与△DEF的周长比为1:2④△ABC与△DEF的面积比为4:1.
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省南部的南宫山景区,为吸引游客组团来此旅游特推出了如下门票收费标准:
标准一:如果人数不超过20人,门票价格70元/人
标准二:如果人数超过20人,每超过1人,门票价格降低2元,但门票价格不低于55元/人
(1)若某单位组织22名员工去南宫山景区旅游,则购买门票共需多少元?
(2)若某单位共支付南宫山景区门票费用1500元,试求该单位这次共有多少名员工去南宫山旅游.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com