练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】关于反比例函数，下列说法不正确的是（　　）

    A. 函数图象分别位于第一、第三象限

    B. 当x＞0时，y随x的增大而减小

    C. 若点A（x1，y1），B（x2，y2）都在函数图象上，且x1＜x2，则y1＞y2

    D. 函数图象经过点（1，2）

    【答案】C

    【解析】

    根据反比例函数图象上点的坐标特征对D进行判断；根据反比例函数的性质对A、B、C进行判断．

    A．k=2＞0，则双曲线的两支分别位于第一、第三象限，所以A选项的说法正确；

    B．当x＞0时，y随着x的增大而减小，所以B选项的说法正确；

    C．若x1＜0，x2＞0，则y2＞y1，所以C选项的说法错误；

    D．把x=1代入得y=2，则点（1，2）在的图象上，所以D选项的说法正确．

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某商店分两次购进A、B两种商品进行销售，每次购进同一种商品的进价相同，具体情况如下表所示：

    （1）求A、B两种商品每件的进价分别是多少元？

    （2）商店计划用5300元的资金进行第三次进货，共进A、B两种商品100件，其中要求B商品的数量不少于A商品的数量，有几种进货方案？

    （3）综合考虑（2）的情况，商店计划对第三次购进的100件商品全部销售，A商品售价为30元/件，每销售一件A商品需捐款a元（1≤a≤10）给希望工程，B商品售价为100元/件，每销售一件B商品需捐款b元给希望工程，a+b＝14．直接写出当b＝　 　时，销售利润最大，最大利润为　 　元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数的图象如图所示，则下列结论：①；②；③当时，：④方程有两个大于-1的实数根.其中正确的是（ ）

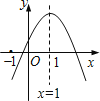
    A.①②③B.①②④C.②③④D.①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，2分别是某款篮球架的实物图与示意图，已知底座BC=0.60米，底座BC与支架AC所成的角∠ACB=75°，支架AF的长为2.50米，篮板顶端F点到篮框D的距离FD=1.35米，篮板底部支架HE与支架AF所成的角∠FHE=60°，求篮框D到地面的距离（精确到0.01米）（参考数据：cos75°≈0.2588，sin75°≈0.9659，tan75°≈3.732，≈1.732，≈1.414）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

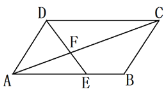
    【题目】如图,在□ABCD中,点E是AB上一点，且AE＝2EB .

    （1）求的值.

    （2）求的值.

    （3）如果△AEF的面积＝8cm2,分别求出△CDF的面积和△ADF的面积

    查看答案和解析>>

    科目：初中数学 来源： 题型：

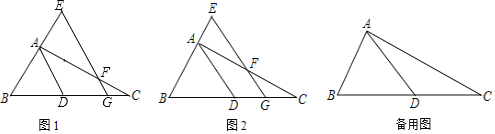
    【题目】如图，Rt△ABC中，∠BAC＝90°，AB＝2，AC＝4，D是BC边上一点，且BD＝CD，G是BC边上的一动点，GE∥AD分别交直线AC，AB于F，E两点．

    （1）AD＝　 　；

    （2）如图1，当GF＝1时，求的值；

    （3）如图2，随点G位置的改变，FG+EG是否为一个定值？如果是，求出这个定值，如果不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（10分）水果店张阿姨以每斤2元的价格购进某种水果若干斤，然后以每斤4元的价格出售，每天可售出100斤，通过调查发现，这种水果每斤的售价每降低0.1元，每天可多售出20斤，为保证每天至少售出260斤，张阿姨决定降价销售．

    （1）若将这种水果每斤的售价降低x元，则每天的销售量是 斤（用含x的代数式表示）；

    （2）销售这种水果要想每天盈利300元，张阿姨需将每斤的售价降低多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

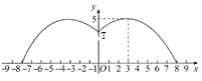
    【题目】有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的立杆上点T处汇合.如图所示为截面图,以水平方向为x轴,喷水池中心为原点建立直角坐标系

    (1)求水柱所在抛物线(第一象限部分)的函数解析式

    (2)正在喷水时,身高1.8米的人,应站在离水池中心多远的地方就能不被淋湿？

    (3)在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心的立杆上点T处汇合,请探究扩建后喷水池水柱的最大高度

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：在平面直角坐标系中，抛物线（）交x轴于A、B两点，交y轴于点C，且对称轴为直线x=-2 .

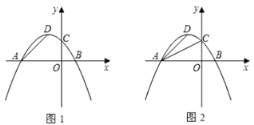
    （1）求该抛物线的解析式及顶点D的坐标；

    （2）若点P(0,t)是y轴上的一个动点，请进行如下探究：

    探究一：如图1，设△PAD的面积为S，令W＝t·S，当0＜t＜4时，W是否有最大值？如果有，求出W的最大值和此时t的值；如果没有，说明理由；

    探究二：如图2，是否存在以P、A、D为顶点的三角形与Rt△AOC相似？如果存在，求点P的坐标；如果不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案