
【题目】如图,⊙O的半径为2,O到顶点A的距离为5,点B在⊙O上,点P是线段AB的中点,若B在⊙O上运动一周.
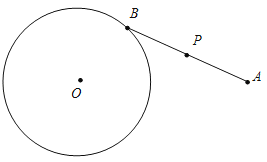
(1)点P的运动路径是一个圆;
(2)△ABC始终是一个等边三角形,直接写出PC长的取值范围.
【答案】(1)见解析;(2)![]() ≤PC≤
≤PC≤![]()
【解析】
(1)连接OA、OB,取OA的中点H,连接OB,HP,则HP是△ABO的中位线,得出HP=![]() OB=1,即P点到H点的距离固定为1,即可得出结论;
OB=1,即P点到H点的距离固定为1,即可得出结论;
(2)由等边三角形的性质和直角三角形的性质分别求出PC的最小值和最大值即可.
(1)解:连接OA、OB,取OA的中点H,连接HP,如图1所示:
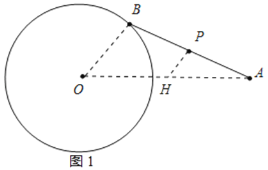
则HP是△ABO的中位线,
∴HP=![]() OB=1,
OB=1,
∴P点到H点的距离固定为1,
∴B在⊙O上运动一周,点P运动的路径是以点H为圆心,半径为1的一个圆;
(2)解:连接AO并延长AO交⊙O于点M、N,如图2所示:
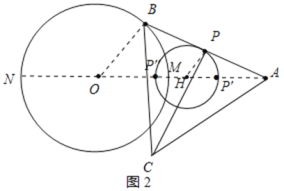
∵△ABC是等边三角形,点P是线段AB的中点,
∴PC⊥AB,PA=PB=![]() AB=
AB=![]() BC,
BC,
∴PC=![]() PA=
PA=![]() AB,
AB,
当点B运动到点M位置时,点P运动到点P'位置,PC最短,
∵AM=OA﹣OM=5﹣2=3,
∴AP'=![]() AM=
AM=![]() ,
,
∴PC=![]() ;
;
当点B运动到点N位置时,点P运动到点P'位置,PC最长,
∵AN=OA+ON=5+2=7,
∴AP'=![]() AN=
AN=![]() ,
,
∴PC=![]() ;
;
∴PC长的取值范围是![]() ≤PC≤
≤PC≤![]() .
.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
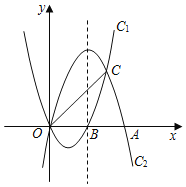
【题目】如图,抛物线C1:y=x2﹣2x与抛物线C2:y=ax2+bx开口大小相同、方向相反,它们相交于O,C两点,且分别与x轴的正半轴交于点B,点A,OA=2OB.
(1)求抛物线C2的解析式;
(2)在抛物线C2的对称轴上是否存在点P,使PA+PC的值最小?若存在,求出点P的坐标,若不存在,说明理由;
(3)M是直线OC上方抛物线C2上的一个动点,连接MO,MC,M运动到什么位置时,△MOC面积最大?并求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(0,2),B(2,2),C(-1,-2),抛物线F:![]() 与直线x=-2交于点P.
与直线x=-2交于点P.
(1)当抛物线F经过点C时,求它的表达式;
(2)设点P的纵坐标为![]() ,求
,求![]() 的最小值,此时抛物线F上有两点
的最小值,此时抛物线F上有两点![]() ,
,![]() ,且
,且![]() ≤-2,比较
≤-2,比较![]() 与
与![]() 的大小;
的大小;
(3)当抛物线F与线段AB有公共点时,直接写出m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=x2+2x﹣3.
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
抛物线C:y=x2+2x﹣3 | A(_____) | B(_____) | (1,0) | (0,﹣3) |
变换后的抛物线C1 | ______ | ______ | ______ | ______ |
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中画出抛物线C.
(2)将抛物线C上每一点的横坐标变为原来的2倍,纵坐标变为原来的![]() ,可证明得到的曲线仍是抛物线,(记为C1),求抛物线C1对应的函数表达式.
,可证明得到的曲线仍是抛物线,(记为C1),求抛物线C1对应的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
定义:与圆的所有切线和割线都有公共点的几何图形叫做这个圆的关联图形.
问题:⊙O的半径为1,画一个⊙O的关联图形.
在解决这个问题时,小明以O为原点建立平面直角坐标系xOy进行探究,他发现能画出很多⊙O的关联图形,例如:⊙O本身和图1中的△ABC(它们都是封闭的图形),以及图2中以O为圆心的![]() (它是非封闭的形),它们都是⊙O的关联图形.而图2中以P,Q为端点的一条曲线就不是⊙O的关联图形.
(它是非封闭的形),它们都是⊙O的关联图形.而图2中以P,Q为端点的一条曲线就不是⊙O的关联图形.
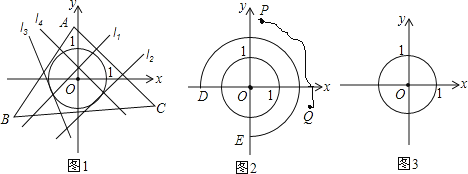
参考小明的发现,解决问题:
(1)在下列几何图形中,①⊙O的外切正多边形;②⊙O的内接正多边形;③⊙O的一个半径大于1的同心圆;⊙O的关联图形是______(填序号).
(2)若图形G是⊙O的关联图形,并且它是封闭的,则图形G的周长的最小值是____.
(3)在图2中,当⊙O的关联图形![]() 的弧长最小时,经过D,E两点的直线为y=____.
的弧长最小时,经过D,E两点的直线为y=____.
(4)请你在备用图中画出一个⊙O的关联图形,所画图形的长度l小于(2)中图形G的周长的最小值,并写出l的值(直接画出图形,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个如图所示的面积为300m2的长方形围栏,围栏总长50m,一边靠墙(墙长25m).
(1)求围栏的长和宽;
(2)能否围成面积为400m2的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
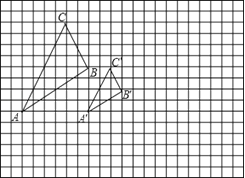
(1)画出位似中心点O;
(2)直接写出△ABC与△A′B′C′的位似比_______
(3)以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A′B′C′关于点O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标._______;_______;_______
查看答案和解析>>
科目:初中数学 来源: 题型:
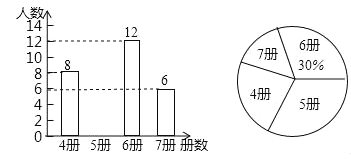
【题目】高尔基说:“书,是人类进步的阶梯.”阅读可以丰富知识、拓展视野、充实生活等诸多益处.为了解学生的课外阅读情况,某校随机抽查了部分学生阅读课外书册数的情况,并绘制出如下统计图,其中条形统计图因为破损丢失了阅读5册书数的数据.
(1)求条形图中丢失的数据,并写出阅读书册数的众数和中位数;
(2)根据随机抽查的这个结果,请估计该校1200名学生中课外阅读5册书的学生人数;
(3)若学校又补查了部分同学的课外阅读情况,得知这部分同学中课外阅读最少的是6册,将补查的情况与之前的数据合并后发现中位数并没有改变,试求最多补查了多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.

(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com