
【题目】如图,在△ABC中,AB=c,AC=b.AD是△ABC的角平分线,DE⊥A于E,DF⊥AC于F,EF与AD相交于O,已知△ADC的面积为1.
(1)证明:DE=DF;
(2)试探究线段EF和AD是否垂直?并说明理由;
(3)若△BDE的面积是△CDF的面积2倍.试求四边形AEDF的面积.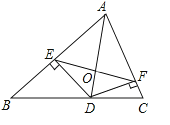
【答案】解:
(1)证明:
∵AD是△ABC的角平分线,DE⊥A于E,DF⊥AC于F,
∴DE=DF(角平分线的性质);
(2)垂直.理由如下:
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中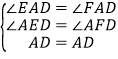 ,
,
∴Rt△AED≌Rt△AFD(AAS),
∴AE=AF,
∴点A在线段EF的垂直平分线上,
同理点D也在线段EF的垂直平分线上,
∴AD⊥EF;
(3)设S△CDF=x,则S△BDE=2x,
∵S△ACD=1,且△AED≌△AFD,
∴S△AED=S△AFD=1﹣x,
∴S△ABD=S△BDE+S△AED=2x+1﹣x=x+1,
又S△ABD=![]() ABDE,S△ACD=
ABDE,S△ACD=![]() ACDF,且AB=c,AC=b,
ACDF,且AB=c,AC=b,
∴![]() ×cDE=x+1,
×cDE=x+1,![]() ×bDF=1,
×bDF=1,
∴DE=![]() ,DF=
,DF=![]() ,
,
又由(1)可知DE=DF,
∴![]() =
=![]() ,解得x=
,解得x=![]() ﹣1,
﹣1,
∵△AED≌△AFD,
∴S△AED=S△AFD=S△ACD﹣S△CDF=1﹣x,
∴S四边形AEDF=2S△AED=2(1﹣x)=2[1﹣(![]() ﹣1)]=4﹣
﹣1)]=4﹣![]() ,
,
即四边形AEDF的面积为4﹣![]() .
.
【解析】(1)由角平分线的性质直接可得到DE=DF;
(2)可证明△AED≌△AFD,可知AE=AF,利用线段垂直平分线的判定可证明AD是EF的垂直平分线,可证得结论;
(3)设△CDF的面积为x,则可分别表示出△BED、△ADE的面积,利用三角形的面积可分别表示出DE和DF,根据DE=DF可得到关于x的方程,可求得x的值,进一步可求得四边形AEDF的面积.
【考点精析】解答此题的关键在于理解三角形三边关系的相关知识,掌握三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】将下列各数填在相应的集合里.
﹣3.8,﹣10,4.3,﹣|﹣ ![]() |,42 , 0,﹣(﹣
|,42 , 0,﹣(﹣ ![]() )
)
整数集合:{ …};
分数集合:{ …};
正数集合:{ …};
负数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了打造区域中心城市,实现跨越式发展,我市新区建设正按投资计划有序推进.新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:
租金(单位:元/台时) | 挖掘土石方量(单位:m3/台时) | |
甲型挖掘机 | 100 | 60 |
乙型挖掘机 | 120 | 80 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题的逆命题是假命题的是( )
A. 对顶角相等 B. 角平分线上的点到这个角的两边的距离相等
C. 如果a2=b2,那么a=b D. 同旁内角互补,两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明过程. 如图,已知∠1+∠2=180°∠B=∠DEF,求证:DE∥BC.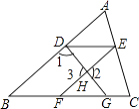
证明:∵∠1+∠2=180°(已知)
∠2=∠3()
∴∠1+∠3=180°
∴∥()
∴∠B=()
∵∠B=∠DEF(已知)
∴∠DEF=()
∴DE∥BC(内错角相等,两直线平行)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com