
ЁОЬтФПЁПЮЊСЫДђдьЧјгђжааФГЧЪаЃЌЪЕЯжПчдНЪНЗЂеЙЃЌЮвЪааТЧјНЈЩше§АДЭЖзЪМЦЛЎгаађЭЦНјЃЎаТЧјНЈЩшЙЄГЬВПЃЌвђЕРТЗНЈЩшашвЊПЊЭкЭСЪЏЗНЃЌМЦЛЎУПаЁЪБЭкОђЭСЪЏЗН540m3 ЃЌ ЯжОіЖЈЯђФГДѓаЭЛњаЕзтСоЙЋЫОзтгУМзЁЂввСНжжаЭКХЕФЭкОђЛњРДЭъГЩетЯюЙЄзїЃЌзтСоЙЋЫОЬсЙЉЕФЭкОђЛњгаЙиаХЯЂШчБэЃК
зтН№ЃЈЕЅЮЛЃКдЊ/ЬЈЪБЃЉ | ЭкОђЭСЪЏЗНСПЃЈЕЅЮЛЃКm3/ЬЈЪБЃЉ | |
МзаЭЭкОђЛњ | 100 | 60 |
вваЭЭкОђЛњ | 120 | 80 |
ЃЈ1ЃЉШєзтгУМзЁЂввСНжжаЭКХЕФЭкОђЛњЙВ8ЬЈЃЌЧЁКУЭъГЩУПаЁЪБЕФЭкОђСПЃЌдђМзЁЂввСНжжаЭКХЕФЭкОђЛњИїашЖрЩйЬЈЃП
ЃЈ2ЃЉШчЙћУПаЁЪБжЇИЖЕФзтН№ВЛГЌЙ§850дЊЃЌгжЧЁКУЭъГЩУПаЁЪБЕФЭкОђСПЃЌФЧУДЙВгаМИжжВЛЭЌЕФзтгУЗНАИЃП
ЁОД№АИЁП
ЃЈ1ЃЉ
ЃЈ1ЃЉЩшМзЁЂввСНжжаЭКХЕФЭкОђЛњИїашxЬЈЁЂyЬЈЃЎ
вРЬтвтЕУЃК![]()
НтЕУ ![]()
Д№ЃКМзЁЂввСНжжаЭКХЕФЭкОђЛњИїаш5ЬЈЁЂ3ЬЈЃЛ
ЃЈ2ЃЉ
ЩшзтгУmЬЈМзаЭЭкОђЛњЃЌnЬЈвваЭЭкОђЛњЃЎ
вРЬтвтЕУЃК60m+80n=540ЃЈmЃЌnОљЮЊздШЛЪ§ЃЉЃЌ
Ёрm=9-![]() n
n
ЁрЗНГЬЕФНтЮЊ![]() ,
,![]() ,
,![]() ЃЎ
ЃЎ
ЕБm=9ЃЌn=0ЪБЃЌжЇИЖзтН№ЃК100ЁС9+120ЁС0=900дЊЃО850дЊЃЌГЌГіЯоЖюЃЛ
ЕБm=5ЃЌn=3ЪБЃЌжЇИЖзтН№ЃК100ЁС5+120ЁС3=860дЊЃО850дЊЃЌГЌГіЯоЖюЃЛ
ЕБm=1ЃЌn=6ЪБЃЌжЇИЖзтН№ЃК100ЁС1+120ЁС6=820дЊЃЌЗћКЯвЊЧѓЃЎ
Д№ЃКгавЛжжзтГЕЗНАИЃЌМДзтгУ1СОМзаЭЭкОђЛњКЭ6СОвваЭЭкОђЛњЃЎ
ЁОНтЮіЁПЃЈ1ЃЉИљОнЕШСПЙиЯЕСаГіЗНГЬзщЃКСНжжЕФЬЈЪ§КЭ=8ЃЛМзаЭЕФСОЪ§ЁСМзаЭУПаЁЪБЕФЭкОђСП+вваЭЕФСОЪ§ЁСвваЭУПаЁЪБЕФЭкОђСП=540ЃЛ
ЃЈ2ЃЉЩшзтгУmЬЈМзаЭЭкОђЛњЃЌnЬЈвваЭЭкОђЛњЃЎвРЬтвтЕУЃК60m+80n=540ЃЈmЃЌnОљЮЊздШЛЪ§ЃЉЃЌЧѓГіmЃЌnЕФе§ећЪ§НтЃЌдйЗжБ№ЧѓГізтН№зїБШНЯ.


 ЭЌВНСЗЯАКгФЯДѓбЇГіАцЩчЯЕСаД№АИ
ЭЌВНСЗЯАКгФЯДѓбЇГіАцЩчЯЕСаД№АИ ЭЌВНСЗЯАЮїФЯДѓбЇГіАцЩчЯЕСаД№АИ
ЭЌВНСЗЯАЮїФЯДѓбЇГіАцЩчЯЕСаД№АИ ВЙГфЯАЬтНЫеЯЕСаД№АИ
ВЙГфЯАЬтНЫеЯЕСаД№АИ бЇСЗПьГЕЕРПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
бЇСЗПьГЕЕРПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЗНГЬ5(2xЃЋ5)2ЃЋ(3xЃ4)(Ѓ3xЃ4)ЃН11x2ЃЋ50xЃЋ41ЕФНтЪЧЃЈ ЃЉ
A. xЃН2 B. xЃНЃ2 C. xЃНЁР2 D. дЗНГЬЮоНт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП[ЃЈЉ1ЃЉn+1p2]nЕШгкЃЈЁЁЁЁЃЉ
A. p2n B. Љp2n C. Љpn+2 D. ЮоЗЈШЗЖЈЁф
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯШЛЏМђЃЌдйЧѓжЕЃК(xЃЋ2)(xЃ2)ЃЋx(1Ѓx)ЃЌЦфжаxЃНЃ1.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћДњЪ§ЪНЉa2+3aЉ2ЕФжЕЕШгк7ЃЌдђДњЪ§ЪН3a2Љ9a+3ЕФжЕЮЊЃЈ ЃЉ
A.24
B.Љ24
C.Љ27
D.27
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЄГЇГаНгСЫвЛХњжНЯфМгЙЄШЮЮёЃЌгУШчЭМ1ЫљЪОЕФГЄЗНаЮКЭе§ЗНаЮжНАхЃЈГЄЗНаЮЕФПэгые§ЗНаЮЕФБпГЄЯрЕШЃЉМгЙЄГЩШчЭМЫљЪОЕФЪњЪНгыКсЪНСНжжЮоИЧЕФГЄЗНаЮжНЯфЃЎЃЈМгЙЄЪБНгЗьВФСЯВЛМЦЃЉ
ЃЈ1ЃЉШєИУГЇЙКНје§ЗНаЮжНАх1000еХЃЌГЄЗНаЮжНАх2000еХЃЎЮЪЪњЪНжНКаЃЌКсЪНжНКаИїМгЙЄЖрЩйИіЃЌЧЁКУФмНЋЙКНјЕФжНАхШЋВПгУЭъ;
ЃЈ2ЃЉИУЙЄГЇФГвЛЬьЪЙгУЕФВФСЯЧхЕЅЩЯЯдЪОЃЌетЬьвЛЙВЪЙгУе§ЗНаЮжНАх50еХЃЌГЄЗНаЮжНАхaеХЃЌШЋВПМгЙЄГЩЩЯЪіСНжжжНКаЃЌЧв120ЃМaЃМ136ЃЌЪдЧѓдкетвЛЬьМгЙЄСНжжжНКаЪБЃЌaЕФЫљгаПЩФмжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
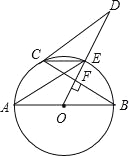
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌODЁЭЯвBCгкЕуFЃЌНЛЁбOгкЕуEЃЌСЌНсCEЁЂAEЁЂCDЃЌШєЁЯAEC=ЁЯODCЃЎ
ЃЈ1ЃЉЧѓжЄЃКжБЯпCDЮЊЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєAB=5ЃЌBC=4ЃЌЧѓЯпЖЮCDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГЄЗНаЮЕФУцЛ§ЪЧ3x2y2Ѓ3xyЃЋ6yЃЌПэЮЊ3yЃЌдђГЄЗНаЮЕФГЄЪЧ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНёЯФЃЌЪЎбпЪаЭѕМвКгДхЙЯЙћЯВЛёЗсЪеЃЌЙћХЉЭѕЖўХжЪеЛёЮїЙЯ20ЖжЃЌЯуЙЯ12ЖжЃЌЯжМЦЛЎзтгУМзЁЂввСНжжЛѕГЕЙВ8СОНЋетХњЙЯЙћШЋВПдЫЭљЭтЕиЯњЪлЃЌвбжЊвЛСОМзжжЛѕГЕПЩзАЮїЙЯ4ЖжКЭЯуЙЯ1ЖжЃЌвЛСОввжжЛѕГЕПЩзАЮїЙЯКЭЯуЙЯИї2ЖжЃЎ
ЃЈ1ЃЉЙћХЉЭѕЖўХжШчКЮАВХХМзЁЂввСНжжЛѕГЕПЩвЛДЮадЕидЫЕНЯњЪлЕиЃПгаМИжжЗНАИЃП
ЃЈ2ЃЉШєМзжжЛѕГЕУПСОвЊИЖдЫЪфЗб300дЊЃЌввжжЛѕГЕУПСОвЊИЖдЫЪфЗб240дЊЃЌдђЙћХЉЭѕЖўХжгІбЁдёФФжжЗНАИЃЌЪЙдЫЪфЗбзюЩйЃПзюЩйдЫЗбЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com