
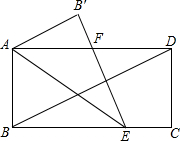
 如图,在矩形ABCD中,AD=2AB,将矩形沿AE折叠,使B落到B′的位置,并且B′E与对角线BD垂直.
如图,在矩形ABCD中,AD=2AB,将矩形沿AE折叠,使B落到B′的位置,并且B′E与对角线BD垂直.| AB′ |
| B′F |
| AD |
| AB |
| 1 |
| 2 |
| ||
| 2 |
 解:(1)如图,∵四边形ABCD为矩形,
解:(1)如图,∵四边形ABCD为矩形,| AB′ |
| B′F |
| AD |
| AB |
| 1 |
| 2 |
| ||
| 2 |
| AF•AB |
| 2 |
| ||
| 4 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
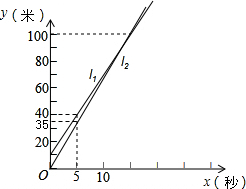 小明和小亮进行百米赛跑,小明比小亮跑得快,如果两人同时起跑,小明肯定赢,现在小明让小亮先跑若干米,两人的路程y(米)分别与小明追赶时间x(秒)的函数关系如图所示.
小明和小亮进行百米赛跑,小明比小亮跑得快,如果两人同时起跑,小明肯定赢,现在小明让小亮先跑若干米,两人的路程y(米)分别与小明追赶时间x(秒)的函数关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com