练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如果x=1是方程ax2+bx+3=0的一个根，求（a-b）2+4ab的值．

    【答案】9

    【解析】

    首先将已知方程的根代入方程求得a、b的和，然后代入已知的代数式求值即可．

    ∵x=1是方程ax2+bx+3=0的一个根，

    ∴a+b=3，

    ∴(ab) 2+4ab=(a+b) 2=(3) 2=9

    故答案为9

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在实数范围内定义一种运算规定a※b=a2-b2，则方程（x+2）※5=0的解为

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：（﹣2）3÷4×（﹣1）100×5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）﹣xy2（x+y）3+x（x+y）2的公因式是__；

    （2）4x（m﹣n）+8y（n﹣m）2的公因式是__．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果等腰三角形一腰上的高与另一腰的夹角为45°，那么这个等腰三角形的底角度数为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将一张长方形纸片与一张直角三角形纸片(∠EFG＝90°)按如图所示的位置摆放，
    使直角三角形纸片的一个顶点E恰好落在长方形纸片的一边AB上，已知∠BEF＝21°，则
    ∠CMF＝ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，E是直线AB，CD内部一点，AB∥CD，连接EA，ED．

    （1）探究猜想：
    ①若∠A=20°，∠D=40°，则∠AED=
    ②猜想图①中∠AED，∠EAB，∠EDC的关系，并用两种不同的方法证明你的结论．
    （2）拓展应用：
    如图②，射线FE与l1 ， l2交于分别交于点E、F，AB∥CD，a，b，c，d分别是被射线FE隔开的4个区域（不含边界，其中区域a，b位于直线AB上方，P是位于以上四个区域上的点，猜想：∠PEB，∠PFC，∠EPF的关系（任写出两种，可直接写答案）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠A=30°，∠B=70°，CE平分∠ACB，CD⊥AB于D，DF⊥CE，求∠CDF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形OABC是一张放在平面直角坐标系中的矩形纸片，点A在x轴上，点C在y轴上，且线段OA、OC（OA＞OC）是方程x2﹣18x+80=0的两根，将边BC折叠，使点B落在边OA上的点D处．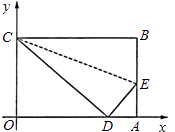

    （1）求线段OA、OC的长；
    （2）求直线CE与x轴交点P的坐标及折痕CE的长；
    （3）是否存在过点D的直线l，使直线CE与x轴所围成的三角形和直线l、直线CE与y轴所围成的三角形相似？如果存在，请直接写出其解析式并画出相应的直线；如果不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案