
����Ŀ����ͼ���ı���OABC��һ�ŷ���ƽ��ֱ������ϵ�еľ���ֽƬ����A��x���ϣ���C��y���ϣ����߶�OA��OC��OA��OC���Ƿ���x2��18x+80=0������������BC�۵���ʹ��B���ڱ�OA�ϵĵ�D����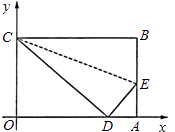
��1�����߶�OA��OC�ij���
��2����ֱ��CE��x�ύ��P�����꼰�ۺ�CE�ij���
��3���Ƿ���ڹ���D��ֱ��l��ʹֱ��CE��x����Χ�ɵ������κ�ֱ��l��ֱ��CE��y����Χ�ɵ����������ƣ�������ڣ���ֱ��д�������ʽ��������Ӧ��ֱ�ߣ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺����x2��18x+80=0��
��ʽ�ֽ�ã���x��8����x��10��=0��
��x��8=0��x��10=0��
��ã�x1=8��x2=10��
��OA=10��OC=8
��2��
�⣺���۵���֪����EBC�ա�EDC����EB=ED��
��CB=CD���־���OABC����AB=OC=8��
��CB=CD=OA=10����OC=8��
��Rt��OCD�У����ݹ��ɶ����ã�OD= ![]() =6��
=6��
��AD=OA��OD=10��6=4��
��BE+EA=AB=8����EB=ED��
��DE+EA=8����DE=8��EA��
��Rt��AED����AE=x����DE=8��x����AD=4��
���ݹ��ɶ����ã���8��x��2=x2+16��
�����ã�16x=48��
��ã�x=3��
��E��������10��3������C��0��8����
��ֱ��CE�Ľ���ʽΪy=kx+b��
��C��E�������ã� ![]() ��
��
��ã�k=�� ![]() ��b=8��
��b=8��
��ֱ��CE����ʽΪy=�� ![]() x+8��
x+8��
��y=0���x=16����P������16��0����
��ʱBE=BA��EA=8��3=5����BC=OA=10��
��Rt��BCE�У����ݹ��ɶ����ã�
CE= ![]() =5
=5 ![]()
��3��
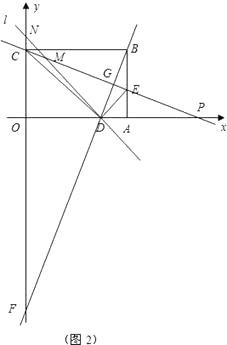
�⣺���ڣ�����������ֱ��l��2����y=��2x+12��y=2x��12��
��ͼ2��
����������1.������ʽ����˷��ѷ�����߷ֽ�Ϊ��һ����ʽ������ʽ��Ȼ�����������˻�Ϊ0��������������һ��Ϊ0��ת��Ϊ����һԪһ�η��̣��ֱ�������̵Ľ�õ�ԭ���̵Ľ⣬����OA����OC�����ɵõ�OA��OC�ij�����2.�����۵���֪������EBC��������EDCȫ�ȣ�����ȫ�������εĶ�Ӧ����ȵõ�EB=ED��CB=CD���־���ABCD�Ա���ȣ��Ӷ��õ�CD�ij�������OC�ij������ù��ɶ������OD�ij����������AD�ij�����ֱ��������AED�У���EA=x����DE=8��x������AD�ij������ù��ɶ����г�����x�ķ��̣�������̵Ľ�õ�AE�ij�����ΪE�������꣬��OA�ij���ΪE�ĺ����꣬ȷ����E�����꣬ͬʱ�õ�BE�ij�������BC�ij�����ֱ��������BCE�У����ù��ɶ�������ۺ�CE�ij���
��3.�����ڣ�Ӧ����������ͼ��
��ֱ��BF�������۵������ʿ�֪CE�ش�ֱƽ��BD����ô��DGP=��CGF=90�㣬����CFG=��DPG�����ǡ�OCP����ǣ����ɴ˿ɵó������������ƣ���ô�ɸ���B��D��������������ֱ�ߵĽ���ʽ��
��ֱ��DN�����ڡ�FCO=��NDO����ô�ɸ��ݡ�OCE����BEC������ֵ�������NDO������ֵ��Ȼ����OD�ij����ON��ֵ���������N������꣬Ȼ�����N��D������������ֱ��DN�Ľ���ʽ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC����AD��AB��BC���ӳ����ڵ�D����CE��AC����ʹAE��BD������DE��
��1����֤��AD=CE��
��2����DE=3��CE=4����tan��DAE��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������������У�ÿ��С�����εı߳���Ϊ1��ÿ��С�����εĶ����Ϊ��㣮���ڸ�����5��5�������������У��Ը��Ϊ���㣬�������������Σ�һ�������εij��ֱ��� ![]() ��2��
��2�� ![]() ����һ�������ε����߳��ֱ���
����һ�������ε����߳��ֱ��� ![]() ��2
��2 ![]() ��5
��5 ![]() �������������������γ�����ͱ߿����غ��⣬���ಿ�ֲ����غϣ�
�������������������γ�����ͱ߿����غ��⣬���ಿ�ֲ����غϣ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������������У�ÿ��С�����εı߳���Ϊ1����ABC�����������λ����ͼ��ʾ������ABC����һ��ƽ�ƺ�õ���A��B��C�䣬ͼ�б���˵�B�Ķ�Ӧ��B�䣮
��������㻭ͼ��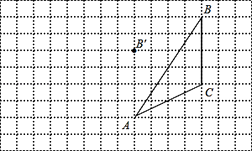
��1��������A��B��C�䣻
��2������AB���ϵ�����CD��
��3������BC���ϵĸ���AE��
��4����A��B��C������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽�����ɣ���ͼ����ֱ֪��m��n��A��BΪֱ��n�ϵ����㣬C��PΪֱ��m�ϵ����㣮 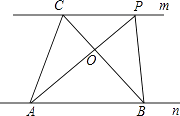
��1����д��ͼ�������ȵĸ��������Σ� ��
��2�����A��B��CΪ�������㣬��P��m���ƶ�����ô����P���ƶ����κ�λ�����У����ABC�������ȣ������ǣ� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��DE��AB��DF��AC��AE=AF�������н��۳������ǣ� �� 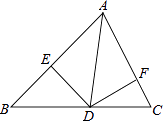
A.BD=CD
B.DE=DF
C.��B=��C
D.AB=AC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������2x2my3��2x4yn�ĺ��ǵ���ʽ����ôm��n���ڣ� ��
A.0
B.1
C.��1
D.��2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com