
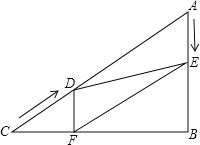
����Ŀ����Rt��ABC�У���B=90����AC=60cm����A=60������D�ӵ�C������CA������4cm/����ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������2cm/����ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t�루0��t��15��������D��DF��BC�ڵ�F������DE��EF������ע����ֱ����������30�Ƚ����Եı���б�ߵ�һ�룩
��1����֤��AE=DF��
��2���ı���AEFD�ܹ���Ϊ����������ܣ������Ӧ��tֵ��������ܣ�˵�����ɣ�
��3����tΪ��ֵʱ����DEFΪֱ�������Σ���˵�����ɣ�
���𰸡���1����֤������������2����t=10����3����t=![]() ��12�����ɼ�����.
��12�����ɼ�����.
�������������������1��������Rt��ABC�����ʵó�AB=30cm������CD=4t��AE=2t�Լ�Rt��CDF�����ʵó��𰸣�
��2��������DF��AB��DF=AE���ó��ı���AEFD��ƽ���ı��Σ��������ε����ʵó�t��ֵ��
��3����������Ҫ����������ֱ���м���.����EDF=90��ʱ��AD=2AE���Ӷ����t��ֵ������DEF=90��ʱ��AE=2AD���Ӷ����t��ֵ.
�����������1��������Rt��ABC�У���C=90�㩁��A=30����
��AB=![]() AC=
AC=![]() ��60=30cm
��60=30cm
��CD=4t��AE=2t�� �֡���Rt��CDF�У���C=30����
��DF=![]() CD=2t
CD=2t
��DF=AE
��2�����ܡ�
��DF��AB��DF=AE�����ı���AEFD��ƽ���ı���
��AD=AEʱ���ı���AEFD�����Σ���60��4t=2t����ã�t=10
�൱t=10ʱ��AEFD������
��3��������DEFΪֱ�������Σ������������
����ͼ1����EDF=90����DE��BC��

��AD=2AE����60��4t=2��2t����ã�t=![]() ��
��
����ͼ2����DEF=90����DE��AC��

��AE=2AD����2t=2��60-4t������ã�t=12��
������������t=![]() ��12ʱ����DEFΪֱ��������
��12ʱ����DEFΪֱ��������


 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
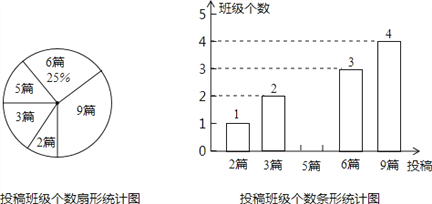
����Ŀ��Ϊ������Ӧ����������������������������ĺ��٣�����ijУ�ڰˣ����꼶��չ���Ļ��Уѧ������������꼶�����ڵ�Ͷ���������ͳ�ƣ����Ƴ�����ͼ��ʾ��������������ͳ��ͼ��
��1��������ͳ��ͼ��Ͷ��ƪ��Ϊ2����Ӧ�����ε�Բ�ĽǵĶ�����
��2�����У�ˣ����꼶��������һ����Ͷ���ƽ��ƪ��������������ͳ��ͼ����������
��3����Ͷ��ƪ��Ϊ9ƪ���ĸ��༶�У��ˣ����꼶���������࣬Уѧ�����������ĸ�����ѡ��������μ�ȫ�еı��ûᣬ�������б�������״ͼ�ķ��������ѡ���������ò���ͬһ�꼶�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�������������ε����֮����1��4����ô�����������ε��ܳ�֮���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���˽�ѧ��ÿ�ܵĿ����Ķ�ʱ���������������˲���ѧ������ѧ��ÿ�ܵĿ����Ķ�ʱ��x����λ��Сʱ�����з�������������������ͼ��ʾ�IJ�������Ƶ���ֲ�ֱ��ͼ������ͳ��ͼ�� 
����ͼ���ṩ����Ϣ������������⣺
��1���������������ѧ���������Ķ�ʱ����6��8Сʱ֮�����ˣ�����ȫƵ���ֲ�ֱ��ͼ
��2��������ͳ��ͼ��m��ֵ��E���Ӧ��Բ�ĽǶ�����
��3������Ƹ�У3000��ѧ��ÿ�ܵĿ����Ķ�ʱ�䲻С��6Сʱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ţ�2���ࡰ����С�顱��5λͬѧ��һ�λ�м�������ϴ��ĸ����ֱ�Ϊ��4��6��8��16��16���������ݵ���λ���������ֱ�Ϊ�� ��
A.16��16
B.10��16
C.8��8
D.8��16
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������ε��ڽǺ�����Ǻ�֮����1800��,��˶������( )
A. �˱��� B. ʮ���� C. ʮ������ D. ʮ�ı���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ�������A��B���������ң��ס��ҡ�������ѧ���������ѡ�����е�һ���������Ķ���
�����¼��У��DZ�Ȼ�¼���Ϊ( )
A.�ס���ͬѧ����A�����ң�B.�ס��ҡ���ͬѧ������������A�����ң�
C.�ס���ͬѧ��ͬһ������D.�ס��ҡ���ͬѧ������������ͬһ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ��ֱ������ϵ�У���P��a��b���ڵ������ޣ���ab��ֵ������Ϊ�� ��
A.5
B.��1
C.��1.5
D.��10
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com