
【题目】市政府为改善居民的居住环境,修建了环境幽雅的环城公园,为了给公园内的草评定期喷水,安装了一些自动旋转喷水器,如图所示,设喷水管![]() 高出地面1.5m,在
高出地面1.5m,在![]() 处有一个自动旋转的喷水头,一瞬间喷出的水流呈抛物线状.喷头
处有一个自动旋转的喷水头,一瞬间喷出的水流呈抛物线状.喷头![]() 与水流最高点
与水流最高点![]() 的连线与地平面成
的连线与地平面成![]() 的角,水流的最高点
的角,水流的最高点![]() 离地平面距离比喷水头
离地平面距离比喷水头![]() 离地平面距离高出2m,水流的落地点为
离地平面距离高出2m,水流的落地点为![]() .在建立如图所示的直角坐标系中:
.在建立如图所示的直角坐标系中:
(1)求抛物线的函数解析式;
(2)求水流的落地点![]() 到
到![]() 点的距离是多少m?
点的距离是多少m?
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
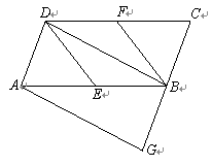
【题目】如图,在□ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,点C是优弧ACB的中点,D、E分别是OA、OB上的点,且AD=BE,弦CM、CN分别过点D、E.
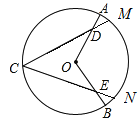
(1)求证:CD=CE.
(2)求证:![]() =
=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,用篱笆靠墙围成矩形花围ABCD,墙可利用的最大长度为15米,一面利用旧墙,其余三面用篱笆围成,篱笆总长为24米.
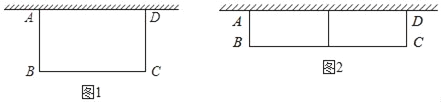
(1)若围成的花圃面积为40米2时,求BC的长;
(2)如图2若计划在花圃中间用一道隔成两个小矩形,且围成的花圃面积为50米2,请你判断能否成功围成花圃,如果能,求BC的长?如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.

(1)求BD的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
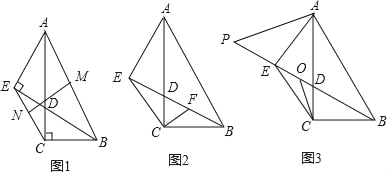
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=2BC,点D在边AC上,连接BD,过A作BD的垂线交BD的延长线于点E.
(1)若M,N分别为线段AB,EC的中点,如图1,求证:MN⊥EC;
(2)如图2,过点C作CF⊥EC交BD于点F,求证:AE=2BF;
(3)如图3,以AE为一边作一个角等于∠BAC,这个角的另一边与BE的延长线交于P点,O为BP的中点,连接OC,求证:OC=![]() (BE﹣PE).
(BE﹣PE).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为5的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.

(1)当BC=6时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EF与AB,CD分别交于点G,H,∠CHG的平分线HM交AB于点M,若∠EGB=50°,则∠GMH的度数为( )

A. 50°B. 55°C. 60°D. 65°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com