
【题目】阅读材料:
如图12-1,过锐角△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:![]() ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.

解答下列问题:
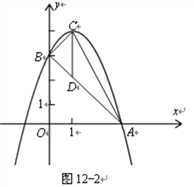
如图12-2,抛物线顶点坐标为点C(1,4),交x轴于点A,交y轴于点B(0,3).
(1)求抛物线解析式和线段AB的长度;
(2)点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及![]() ;
;
(3)是否存在一点P,使S△PAB=![]() S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
【答案】(1)3![]() ;(2)CD=2,3;(3)见解析.
;(2)CD=2,3;(3)见解析.
【解析】(1)已知抛物线的顶点C的坐标,可设这个二次函数的解析式为![]() ,然后把A点坐标代入即可求出二次函数的解析式,继而求出点B坐标,根据勾股定理即可求出AB的长;
,然后把A点坐标代入即可求出二次函数的解析式,继而求出点B坐标,根据勾股定理即可求出AB的长;
(2)求出直线AB的解析式,由C点的横坐标可求得D点的纵坐标,从而可求得CD的长,然后再根据题中给出的求三角形面积的求法进行求解即可得;
(3)可先根据(2)中三角形CAB的面积得出三角形PAB的面积,三角形PAB中,水平宽是A的横坐标为定值,因此根据三角形PAB的面积可得出此时的铅垂高,然后用抛物线的解析式以及一次函数的解析式,先表示出铅垂高,然后根据由三角形PAB的面积求出的铅垂高可得出关于x的方程,即可得出x的值,然后代入二次函数式中即可得出此点的坐标.
(1)设抛物线的解析式为:![]() ,
,
把B(0,3)代入解析式求得![]() ,
,
所以![]() ,
,
由![]() 求得A点的坐标为
求得A点的坐标为![]() ,
,
所以OA=3,OB=3,所以AB=![]() ;
;
(2) 设直线AB的解析式为:![]() ,
,
把A(3,0),B(0,3)代入y2=kx+b中,得![]() ,
,
解得:k=-1,b=3,
所以y2=-x+3,
因为C点坐标为(1,4),
所以当x=1时,y1=4,y2=2,
所以CD=4-2=2,
![]() (平方单位) ;
(平方单位) ;
(3)假设存在符合条件的点P,设P点的横坐标为x,△PAB的铅垂高为h,
则![]() ,
,
由S△PAB=![]() S△CAB得:
S△CAB得:![]() ,
,
化简得:![]() ,
,
△=-36<0,
所以不存在这样的P点.


科目:初中数学 来源: 题型:
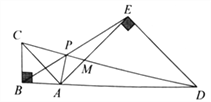
【题目】如图,点![]() 在线段
在线段![]() 上,在
上,在![]() 的同侧作等腰
的同侧作等腰![]() 和等腰
和等腰![]() ,
,![]() 与
与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() .对于下列结论:
.对于下列结论:
①![]() ;②
;②![]() ;③
;③![]() .其中正确的是( )
.其中正确的是( )
A. ①②③ B. ① C. ①② D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射阳县实验初中为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
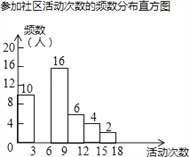
参加社区活动次数的频数、频率分布表
活动次数x | 频数 | 频率 |
0<x≤3 | 10 | 0.20 |
3<x≤6 | a | 0.24 |
6<x≤9 | 16 | 0.32 |
9<x≤12 | 6 | 0.12 |
12<x≤15 | m | b |
15<x≤18 | 2 | n |
根据以上图表信息,解答下列问题:
(1)表中a= ,b= ;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会准备调查2010级初三同学每天(除课间操外)的课外锻炼时间.
(1) 确定调查方式时,甲同学说:“我到(1)班去调查全体同学”;乙同学说:“我到体育场上去询问参加锻炼的同学”;丙同学说:“我到2010级初三每个班去随机调查一定数量的同学”.请你指出哪位同学的调查方式最为合理;
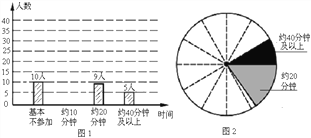
(2) 他们采用了最为合理的调查方法收集数据,并绘制出如图1所示的条形统计图和如图2所示的扇形统计图,请将条形统计图补充完整,并在扇形统计图中涂出一块表示“基本不参加”的部分;
(3) 若该校2010级初三共有240名同学,请你估计其中每天(除课间操外)课外锻炼时间不超过20分钟的人数.(注:图2中相邻两虚线形成的圆心角均为30°)
查看答案和解析>>
科目:初中数学 来源: 题型:
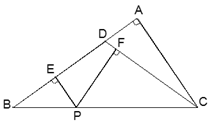
【题目】如图,在△ABC中,∠A=90°, D是AB边上一点,且DB=DC,过BC上一点P(不包括B,C二点)作PE⊥AB,垂足为点E, PF⊥CD,垂足为点F,已知AD:DB=1:4,BC=![]() ,求PE+PF的长.
,求PE+PF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算.
(1)4×(﹣![]() )÷(﹣2)
)÷(﹣2)
(2)![]()
(3)﹣1+(1﹣0.5)÷(﹣3)×[2﹣(﹣3)2]
(4)2(a2﹣ab)+3(![]() a2﹣ab)+4ab
a2﹣ab)+4ab
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点 C为线段 AB上一点,分别以 AC、BC为边在线段 AB同侧作△ACD和△BCE,且 CA=CD,CB=CE,∠ACD=∠BCE,直线 AE与 BD交于点 F
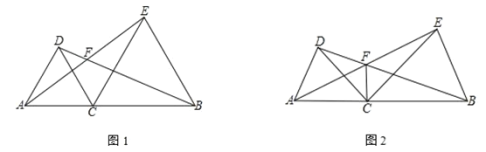
(1)如图 1,若∠ACD=60°,则∠AFD=
(2)如图 2,若∠ACD=α,连接 CF,则∠AFC= (用含α的式子表示)
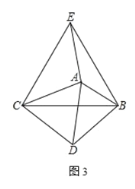
(3) 将图 1 中的△ACD绕点 C顺时针旋转如图 3,连接 AE、AB、BD,∠ABD=80°,求∠EAB的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() .点
.点![]() 从
从![]() 向
向![]() 以每秒
以每秒![]() 个单位的速度运动,以
个单位的速度运动,以![]() 为一边在
为一边在![]() 的右下方作正方形
的右下方作正方形![]() .同时垂直于
.同时垂直于![]() 的直线
的直线![]() 从
从![]() 向
向![]() 以每秒
以每秒![]() 个单位的速度运动,设运动时间为
个单位的速度运动,设运动时间为![]() 秒,当
秒,当![]() ________.秒时,直线
________.秒时,直线![]() 和正方形
和正方形![]() 开始有公共点
开始有公共点
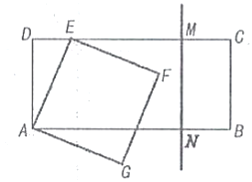
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com