
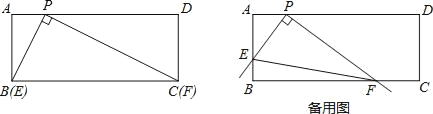
ЁОЬтФПЁПдкОиаЮABCDжаЃЌЕуPдкADЩЯЃЌAB=3ЃЌAP=1ЃЌНЋШ§НЧАхЕФжБНЧЖЅЕуЗХдкЕуPДІЃЌШ§НЧАхЕФСНжБНЧБпЗжБ№ФмгыABЁЂBCБпЯрНЛгкЕуEЁЂFЃЌСЌНгEFЃЎ
ЃЈ1ЃЉШчЭМЃЌЕБЕуEгыЕуBжиКЯЪБЃЌЕуFЧЁКУгыЕуCжиКЯЃЌЧѓДЫЪБPCЕФГЄЃЛ
ЃЈ2ЃЉНЋШ§НЧАхДгЃЈ1ЃЉжаЕФЮЛжУПЊЪМЃЌШЦЕуPЫГЪБеыа§зЊЃЌЕБЕуEгыЕуAжиКЯЪБЭЃжЙЃЌдкетИіЙ§ГЬжаЃЌЧыФуЙлВьЁЂЬНОПВЂНтД№ЃКдкетИіЙ§ГЬжаЃЌЩшCF=mЃЎЪдНтД№ЃКЂйгУКЌmЕФДњЪ§ЪНБэЪОЫФБпаЮBEPFЕФУцЛ§ЃЌВЂжБНгаДГіmЕФШЁжЕЗЖЮЇЃЛЂкДгПЊЪМЕНЭЃжЙЃЌЧѓЯпЖЮEFЕФжаЕуЫљОЙ§ЕФТЗЯпГЄЃЎ

| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACBЃН90ЁуЃЌDЪЧBCЕФжаЕуЃЌDEЁЭBCЃЌCE//ADЃЌШєACЃН2ЃЌCEЃН4ЃЌдђЫФБпаЮACEBЕФжмГЄЮЊ Ёј ЃЎ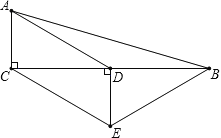
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЪ§бЇПЮЩЯЃЌРЯЪІЬсГівЛИіЮЪЬтЁАгУжБГпКЭдВЙцзївЛИіОиаЮЁБЃЎ
аЁЛЊЕФзіЗЈШчЯТЃК
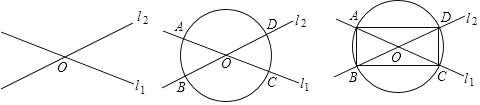
![]() ШчЭМ1ЃЌШЮШЁвЛЕуOЃЌЙ§ЕуOзїжБЯпl1ЃЌl2ЃЛ
ШчЭМ1ЃЌШЮШЁвЛЕуOЃЌЙ§ЕуOзїжБЯпl1ЃЌl2ЃЛ![]() ШчЭМ2ЃЌвдOЮЊдВаФЃЌШЮвтГЄЮЊАыОЖзїдВЃЌгыжБЯпl1ЃЌl2ЗжБ№ЯрНЛгкЕуAЁЂCЃЌBЁЂDЃЛ
ШчЭМ2ЃЌвдOЮЊдВаФЃЌШЮвтГЄЮЊАыОЖзїдВЃЌгыжБЯпl1ЃЌl2ЗжБ№ЯрНЛгкЕуAЁЂCЃЌBЁЂDЃЛ![]() ШчЭМ3ЃЌСЌНгABЁЂBCЁЂCDЁЂDAЫФБпаЮABCDМДЮЊЫљЧѓзїЕФОиаЮЃЎ
ШчЭМ3ЃЌСЌНгABЁЂBCЁЂCDЁЂDAЫФБпаЮABCDМДЮЊЫљЧѓзїЕФОиаЮЃЎ
РЯЪІЫЕЃКЁАаЁЛЊЕФзїЗЈе§ШЗЁБЃЎ
ЧыЛиД№ЃКаЁЛЊЕФзїЭМвРОнЪЧ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABCDЕФжмГЄЮЊ36ЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌЕуEЪЧCDЕФжаЕуЃЌBD=12ЃЌдђЁїDOEЕФжмГЄЮЊЃЈЁЁЁЁЃЉ

A. 15 B. 18 C. 21 D. 24
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
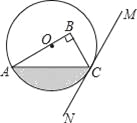
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯB=90ЁуЃЌЕуOдкБпABЩЯЃЌвдЕуOЮЊдВаФЃЌOAЮЊАыОЖЕФдВОЙ§ЕуCЃЌЙ§ЕуCзїжБЯпMNЃЌЪЙЁЯBCM=2ЁЯAЃЎ
ЃЈ1ЃЉХаЖЯжБЯпMNгыЁбOЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєOA=4ЃЌЁЯBCM=60ЁуЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжабыЕчЪгЬЈЕФЁАжаЙњЪЋДЪДѓШќЁБНкФПЮФЛЏЦЗЮЛИпЃЌФкШнЗсИЛЃЌФГаЃГѕЖўФъМЖФЃФтПЊеЙЁАжаЙњЪЋДЪДѓШќЁББШШќЃЌЖдШЋФъМЖЭЌбЇГЩМЈНјааЭГМЦКѓЗжЮЊЁАгХауЁБЁЂЁАСМКУЁБЁЂЁАвЛАуЁБЁЂЁАНЯВюЁБЫФИіЕШМЖЃЌВЂИљОнГЩМЈЛцжЦГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыНсКЯЭГМЦЭМжаЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉЩШаЮЭГМЦЭМжаЁАгХауЁБЫљЖдгІЕФЩШаЮЕФдВаФНЧЮЊ ЖШЃЌВЂНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЎ
ЃЈ2ЃЉДЫДЮБШШќгаЫФУћЭЌбЇЛюЖЏТњЗжЃЌЗжБ№ЪЧМзЁЂввЁЂБћЁЂЖЁЃЌЯжДгетЫФУћЭЌбЇжаЬєбЁСНУћЭЌбЇВЮМгбЇаЃОйааЕФЁАжаЙњЪЋДЪДѓШќЁББШШќЃЌЧыгУСаБэЗЈЛђЛЪїзДЭМЗЈЃЌЧѓГібЁжаЕФСНУћЭЌбЇЧЁКУЪЧМзЁЂЖЁЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСВФСЯЃЌЛиД№ЮЪЬтЃК
аЁДЯбЇЭъСЫЁАШёНЧШ§НЧКЏЪ§ЁБЕФЯрЙижЊЪЖКѓЃЌЭЈЙ§баОПЗЂЯжЃКШчЭМ1ЃЌдкRtЁїABCжаЃЌШчЙћЁЯC=90ЁуЃЌЁЯ=30ЁуЃЌBCЈTa=1ЃЌAC=b=![]() ЃЌAB=c=2ЃЌФЧУД
ЃЌAB=c=2ЃЌФЧУД![]() =
=![]() =2ЃЎЭЈЙ§ЩЯЭјВщдФзЪСЯЃЌЫћгжжЊЁАsin90Ёу=1ЁБЃЌвђДЫЫћЕУЕНЁАдкКЌ30ЁуНЧЕФжБНЧШ§НЧаЮжаЃЌДцдкзХ
=2ЃЎЭЈЙ§ЩЯЭјВщдФзЪСЯЃЌЫћгжжЊЁАsin90Ёу=1ЁБЃЌвђДЫЫћЕУЕНЁАдкКЌ30ЁуНЧЕФжБНЧШ§НЧаЮжаЃЌДцдкзХ![]() =
=![]() =
=![]() ЕФЙиЯЕЃЎ
ЕФЙиЯЕЃЎ
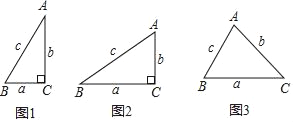
етИіЙиЯЕЖдгквЛАуШ§НЧаЮЛЙЪЪгУТ№ЃПЮЊДЫЫћзіСЫШчЯТЕФЬНОПЃК
ЃЈ1ЃЉШчЭМ2ЃЌдкRЁїABCжаЃЌЁЯC=90ЁуЃЌBC=aЃЌAC=bЃЌAB=CЃЌЧыХаЖЯДЫЪБЁА![]() =
=![]() =
=![]() ЁБЕФЙиЯЕЪЧЗёГЩСЂЃПД№ЃКЁЁ ЁЁ
ЁБЕФЙиЯЕЪЧЗёГЩСЂЃПД№ЃКЁЁ ЁЁ
ЃЈ2ЃЉЭъГЩЩЯЪіЬНОПКѓЃЌЫћгжЯыЁАЖдгкШЮвтЕФШёНЧЁїABCЃЌЩЯЪіЙиЯЕЛЙГЩСЂТ№ЃПЁБвђДЫЫћгжМЬајНјааСЫШчЯТЕФЬНОПЃК
ШчЭМ3ЃЌдкШёНЧЁїABCжаЃЌBC=aЃЌAC=bЃЌAB=cЃЌЧыХаЖЯДЫЪБЁА![]() =
=![]() =
=![]() ЁБЕФЙиЯЕЪЧЗёГЩСЂЃПВЂжЄУїФуЕФХаЖЯЃЎЃЈЬсЪОЃКЙ§ЕуCзїCDЁЭABгкDЃЌЙ§ЕуAзїAHЁЭBCЃЌдйНсКЯЖЈвхЛђЦфЫќЗНЗЈжЄУїЃЉЃЎ
ЁБЕФЙиЯЕЪЧЗёГЩСЂЃПВЂжЄУїФуЕФХаЖЯЃЎЃЈЬсЪОЃКЙ§ЕуCзїCDЁЭABгкDЃЌЙ§ЕуAзїAHЁЭBCЃЌдйНсКЯЖЈвхЛђЦфЫќЗНЗЈжЄУїЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
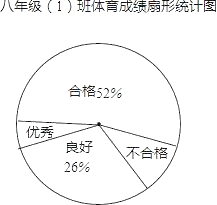
ЁОЬтФПЁПФГаЃЖдОХФъМЖЃЈ1ЃЉАрШЋЬхбЇЩњНјааЬхг§ВтЪдЃЌВтЪдГЩМЈЗжЮЊгХауЁЂСМКУЁЂКЯИёКЭВЛКЯИёЫФИіЕШМЖЃЌИљОнВтЪдГЩМЈЛцжЦЕФВЛЭъећЭГМЦЭМБэШчЯТЃК
ОХФъМЖЃЈ1ЃЉАрЬхг§ГЩМЈЦЕЪ§ЗжВМБэЃК
ЕШМЖ | ЗжжЕ | ЦЕЪ§ |
гХау | ЁЁ90Љ100Зж | |
СМКУ | ЁЁ75Љ89Зж | ЁЁ13 |
КЯИё | ЁЁ60Љ74Зж | |
ВЛКЯИё | ЁЁ0Љ59Зж | ЁЁ9 |
ИљОнЭГМЦЭМБэИјГіЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉОХФъМЖЃЈ1ЃЉАрЙВгаЖрЩйУћбЇЩњЃП
ЃЈ2ЃЉЬхг§ГЩМЈЮЊгХауЕФЦЕЪ§ЪЧЁЁ ЁЁЃЌКЯИёЕФЦЕЪ§ЮЊЁЁ ЁЁЃЛ
ЃЈ3ЃЉШєЖдИУАрЬхг§ГЩМЈДяЕНгХауГЬЖШЕФ3ИіФаЩњКЭ2ИіХЎЩњжаЫцЛњГщШЁ2ШЫВЮМгбЇаЃЬхг§ОКШќЃЌЧЁКУГщЕН1ИіФаЩњКЭ1ИіХЎЩњЕФИХТЪЪЧЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФЦНЗжЯпЃЌ
ЕФЦНЗжЯпЃЌ![]() ЃЌДЙзуЪЧ
ЃЌДЙзуЪЧ![]() ЃЌ
ЃЌ![]() КЭ
КЭ![]() ЕФбгГЄЯпНЛгкЕу
ЕФбгГЄЯпНЛгкЕу![]() ЃЎ
ЃЎ
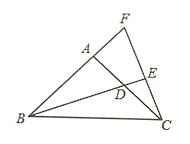
ЃЈ1ЃЉдкЭМжаевГігы![]() ШЋЕШЕФШ§НЧаЮЃЌВЂЫЕГіШЋЕШЕФРэгЩЃЛ
ШЋЕШЕФШ§НЧаЮЃЌВЂЫЕГіШЋЕШЕФРэгЩЃЛ
ЃЈ2ЃЉЫЕУї![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЙћ![]() ЃЌжБНгаДГі
ЃЌжБНгаДГі![]() ЕФГЄЮЊ ЃЎ
ЕФГЄЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com