
����Ŀ��ijУ�Ծ��꼶��1����ȫ��ѧ�������������ԣ����Գɼ���Ϊ���㡢���á��ϸ�Ͳ��ϸ��ĸ��ȼ������ݲ��Գɼ����ƵIJ�����ͳ��ͼ�����£�
���꼶��1���������ɼ�Ƶ���ֲ�����
�ȼ� | ��ֵ | Ƶ�� |
���� | ��90��100�� | |
���� | ��75��89�� | ��13 |
�ϸ� | ��60��74�� | |
���ϸ� | ��0��59�� | ��9 |
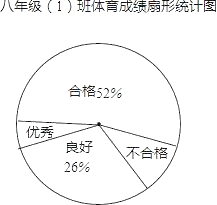
����ͳ��ͼ����������Ϣ������������⣺
��1�����꼶��1����ж�����ѧ����
��2�������ɼ�Ϊ�����Ƶ������ �����ϸ��Ƶ��Ϊ�� ����
��3�����Ըð������ɼ��ﵽ����̶ȵ�3��������2��Ů���������ȡ2�˲μ�ѧУ����������ǡ�ó鵽1��������1��Ů���ĸ������� ����
���𰸡�������
��������
��1�������õ�Ƶ����������ռ�İٷֱȵõ��������������
��2������50��52%�õ��ϸ��Ƶ����Ȼ����50�ֱ��ȥ�����������͵�Ƶ���õ������Ƶ����
��3������״ͼչʾ����20�ֵȿ��ܵĽ�������ҳ�ǡ�ó鵽1��������1��Ů���Ľ������Ȼ����ݸ��ʹ�ʽ�����
��1��13��26%=50�����Ծ��꼶��1�����50��ѧ����
��2��50��52%=26�����ϸ��Ƶ��Ϊ26�����������Ƶ��Ϊ50��13��9��26=2��
��3������״ͼΪ��
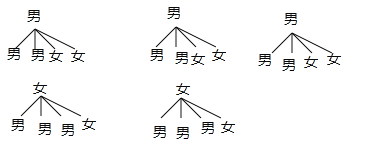
����20�ֵȿ��ܵĽ����������ǡ�ó鵽1��������1��Ů���Ľ����Ϊ12������ǡ�ó鵽1��������1��Ů���ĸ���=![]() =
=![]() ��
��
�ʴ�Ϊ��2��26��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
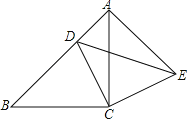
����Ŀ����ͼ����ABC�ǵ���ֱ�������Σ��ҡ�ACB��90�㣬��D��AB���ϵ�һ�㣨��D����A��B�غϣ�������CD������C��CE��CD����CE��CD������DE��AE��
��1����֤����CBD�ա�CAE��
��2����AD��4��BD��8����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
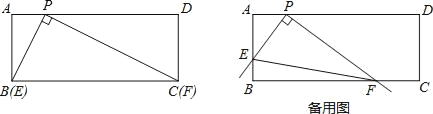
����Ŀ���ھ���ABCD�У���P��AD�ϣ�AB=3��AP=1�������ǰ��ֱ�Ƕ�����ڵ�P�������ǰ����ֱ�DZ߷ֱ�����AB��BC���ཻ�ڵ�E��F������EF��
��1����ͼ������E���B�غ�ʱ����Fǡ�����C�غϣ����ʱPC�ij���
��2�������ǰ�ӣ�1���е�λ�ÿ�ʼ���Ƶ�P˳ʱ����ת������E���A�غ�ʱֹͣ������������У�����۲졢̽�����������������У���CF=m���Խ�𣺢��ú�m�Ĵ���ʽ��ʾ�ı���BEPF���������ֱ��д��m��ȡֵ��Χ���ڴӿ�ʼ��ֹͣ�����߶�EF���е���������·�߳���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��������CEFG�ı߳��ֱ�Ϊa��b��������CEFG�Ƶ�C��ת���������н��ۣ���BE=DG����BE��DG����DE2+BG2=2a2+2b2��������ȷ�����ǣ�������
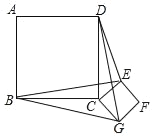
A. ��B. ��C. �٢�D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��б��AF���¶�Ϊ5��12��б��AF��һ����ˮƽ�洹ֱ�Ĵ���BD�����������£���б���ϵ�Ӱ��BC=6.5�ף���ʱ������ˮƽ��ǡ�ó�30��ǣ������BD�ĸߣ��������ȷ��0.1�ף��ο�����![]() ��1.414��
��1.414��![]() ��1.732��
��1.732��
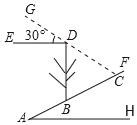
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=![]() ��AC=
��AC=![]() ��BC=
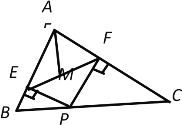
��BC=![]() ��PΪ��BC��һ���㣬PE��AB��E��PF��AC��F��MΪEF�е㣬��AM����СֵΪ__________��
��PΪ��BC��һ���㣬PE��AB��E��PF��AC��F��MΪEF�е㣬��AM����СֵΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD=12��DO=OB=����AC=26����ADB=90��.��BC�ij����ı���ABCD�����.
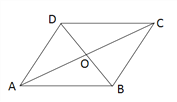
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ӳ���ѵ������Ҫ��Ŀ֮һ������ͼ���е��������˶�Ա�ס��ҡ�������ÿ��10�ε�����Եijɼ������Թ���Ϊÿ����������10����ÿ����λ1����1�֣���֪�˶�Ա�ײ��Գɼ�����λ������������7��
�˶�Ա�ײ��Գɼ�ͳ�Ʊ�
������� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
�ɼ����֣� | 7 | 6 | 8 | 7 |
| 6 | 8 | 6 | 8 |
|
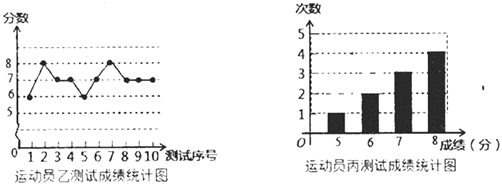
��1����գ�![]() ______��
______��![]() ______��
______��
��2��Ҫ������������ѡ��һλ�����Ϊ�ȶ��Ľ������֣�����Ϊѡ˭�����ʣ�Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() (�����ǵ��ӳ���)�ϵĶ��㣬��
(�����ǵ��ӳ���)�ϵĶ��㣬��![]() ��
��
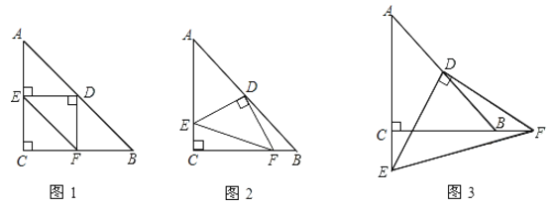
��1����![]() ʱ����ͼ�٣��߶�
ʱ����ͼ�٣��߶�![]() ���߶�
���߶�![]() �Ĺ�ϵ�ǣ�_________________��
�Ĺ�ϵ�ǣ�_________________��
��2����![]() ��
��![]() ����ֱʱ����ͼ�ڣ���1���Ľ��ۻ��������������������֤����������������˵�����ɣ�
����ֱʱ����ͼ�ڣ���1���Ľ��ۻ��������������������֤����������������˵�����ɣ�
��3����![]() ��
��![]() �˶���
�˶���![]() ��
��![]() ���ӳ���ʱ����ͼ�ۣ���ֱ��д��
���ӳ���ʱ����ͼ�ۣ���ֱ��д��![]() ��
��![]() ��
��![]() ֮��Ĺ�ϵ��
֮��Ĺ�ϵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com