
【题目】如图,斜坡AF的坡度为5:12,斜坡AF上一棵与水平面垂直的大树BD在阳光照射下,在斜坡上的影长BC=6.5米,此时光线与水平线恰好成30°角,求大树BD的高.(结果精确的0.1米,参考数据![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
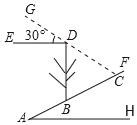
【答案】大树的高约为6.0米.
【解析】
作CM⊥DB于点M,已知BC的坡度即可得到BM和CM的比值,在Rt△MBC中,利用勾股定理即可求得BM和MC的长度,再在Rt△DCM中利用三角函数求得DM的长,由BD=BM+DM即可求得大树BD的高.
作CM⊥DB于点M,
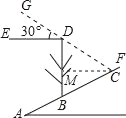
∵斜坡AF的坡度是1::2.4,∠A=∠BCM,
∴![]() =
=![]() =
=![]() ,
,
∴在直角△MBC中,设BM=5x,则CM=12x.
由勾股定理可得:BM2+CM2=BC2,
∴(5x)2+(12x)2=6.52,
解得:x=![]() ,
,
∴BM=5x=![]() ,CM=12x=6,
,CM=12x=6,
在直角△MDC中,∠DCM=∠EDG=30°,
∴DM=CMtan∠DCM=6tan30°=6×![]() =2
=2![]() ,
,
∴BD=DM+BM=![]() +2
+2![]() ≈2.5+2×1.732≈6.0(米).
≈2.5+2×1.732≈6.0(米).
答:大树的高约为6.0米.


科目:初中数学 来源: 题型:
【题目】某公司销售部有营销员15人,销售部为了制定关于某种商品的每位营销员的个人月销售定额,统计了这15人某月关于此商品的个人月销售量(单位:件)如下:
个人月销售量 | 1800 | 510 | 250 | 210 | 150 | 120 |
营销员人数 | 1 | 1 | 3 | 5 | 3 | 2 |
(1)求这15位营销员该月关于此商品的个人月销售量的平均数,并直接写出这组数据的中位数和众数;
(2)假设该销售部负责人把每位营销员关于此商品的个人月销售定额确定为320件,你认为对多数营销员是否合理?并在(1)的基础上说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
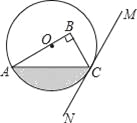
【题目】如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.
(1)判断直线MN与⊙O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,回答问题:
小聪学完了“锐角三角函数”的相关知识后,通过研究发现:如图1,在Rt△ABC中,如果∠C=90°,∠=30°,BC═a=1,AC=b=![]() ,AB=c=2,那么
,AB=c=2,那么![]() =
=![]() =2.通过上网查阅资料,他又知“sin90°=1”,因此他得到“在含30°角的直角三角形中,存在着
=2.通过上网查阅资料,他又知“sin90°=1”,因此他得到“在含30°角的直角三角形中,存在着![]() =
=![]() =
=![]() 的关系.
的关系.
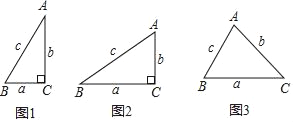
这个关系对于一般三角形还适用吗?为此他做了如下的探究:
(1)如图2,在R△ABC中,∠C=90°,BC=a,AC=b,AB=C,请判断此时“![]() =
=![]() =
=![]() ”的关系是否成立?答:
”的关系是否成立?答:
(2)完成上述探究后,他又想“对于任意的锐角△ABC,上述关系还成立吗?”因此他又继续进行了如下的探究:
如图3,在锐角△ABC中,BC=a,AC=b,AB=c,请判断此时“![]() =
=![]() =
=![]() ”的关系是否成立?并证明你的判断.(提示:过点C作CD⊥AB于D,过点A作AH⊥BC,再结合定义或其它方法证明).
”的关系是否成立?并证明你的判断.(提示:过点C作CD⊥AB于D,过点A作AH⊥BC,再结合定义或其它方法证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
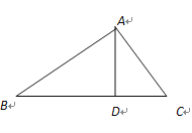
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)求作∠ABC的平分线,分别交AD,AC于E,F两点;(要求:尺规作图,保留作图痕迹,不写作法)
(2)证明:AE=AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
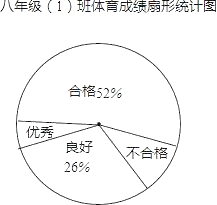
【题目】某校对九年级(1)班全体学生进行体育测试,测试成绩分为优秀、良好、合格和不合格四个等级,根据测试成绩绘制的不完整统计图表如下:
九年级(1)班体育成绩频数分布表:
等级 | 分值 | 频数 |
优秀 | 90﹣100分 | |
良好 | 75﹣89分 | 13 |
合格 | 60﹣74分 | |
不合格 | 0﹣59分 | 9 |
根据统计图表给出的信息,解答下列问题:
(1)九年级(1)班共有多少名学生?
(2)体育成绩为优秀的频数是 ,合格的频数为 ;
(3)若对该班体育成绩达到优秀程度的3个男生和2个女生中随机抽取2人参加学校体育竞赛,恰好抽到1个男生和1个女生的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
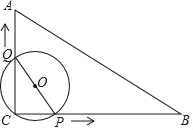
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2cm,AB=4cm,动点P从点C出发,在BC边上以每秒![]() cm的速度向点B匀速运动,同时动点Q也从点C出发,沿C→A→B以每秒4cm的速度匀速运动,运动时间为t秒
cm的速度向点B匀速运动,同时动点Q也从点C出发,沿C→A→B以每秒4cm的速度匀速运动,运动时间为t秒![]() ,连接PQ,以PQ为直径作⊙O.
,连接PQ,以PQ为直径作⊙O.
(1)当![]() 时,求△PCQ的面积;
时,求△PCQ的面积;
(2)设⊙O的面积为s,求s与t的函数关系式;
(3)当点Q在AB上运动时,⊙O与Rt△ABC的一边相切,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
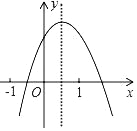
【题目】二次函数y=ax2+bx+c的图象如图示,下列结论:
(1)b<0;(2)c>0;(3)b2﹣4ac>0; (4)a﹣b+c<0,
(5)2a+b<0; (6)abc>0;其中正确的是_____;(填写序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com