
����Ŀ��ij��˾���۲���Ӫ��Ա15�ˣ����۲�Ϊ���ƶ�����ij����Ʒ��ÿλӪ��Ա�ĸ��������۶��ͳ������15��ij�¹��ڴ���Ʒ�ĸ���������������λ���������£�
������������ | 1800 | 510 | 250 | 210 | 150 | 120 |
Ӫ��Ա���� | 1 | 1 | 3 | 5 | 3 | 2 |
��1������15λӪ��Ա���¹��ڴ���Ʒ�ĸ�������������ƽ��������ֱ��д���������ݵ���λ����������
��2����������۲������˰�ÿλӪ��Ա���ڴ���Ʒ�ĸ��������۶���ȷ��Ϊ320��������Ϊ�Զ���Ӫ��Ա�Ƿ���������ڣ�1���Ļ�����˵�����ɣ�
���𰸡���1��ƽ����320����λ��210������210����2�������������ɼ�������
��������
��1������ƽ�����Ķ����Լ����㹫ʽ����λ���Ķ��塢�����Ķ�����⼴�ɣ�
��2������ƽ��������λ���������Ķ�����з������ɣ�
��1��ƽ�����ǣ�![]() ��1800+510+25��3+210��5+150��3+120��2����320��������
��1800+510+25��3+210��5+150��3+120��2����320��������
���е������ǰ��Ӵ�С��˳�����еģ������м�λ�õ���210�������λ����210��������
210������5����࣬����������210��
��2����������
��Ϊ15������13�˵����۶��320����320����������һ�����ݵ�ƽ��������ȴ���ܺܺõط�ӳ������Ա��һ��ˮƽ�����۶Ϊ210������Щ����Ϊ210��������λ���������������Ǵ����ܴﵽ�Ķ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�Ƶ�A˳ʱ����ת������AB��C��D����λ�ã���ת��Ϊ����0��������90����������1=110�������Ϧ�= ��
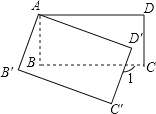
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ��������β��ϣ��ٽ���������⣺
��һ�����⣺�ֽ���ʽ��![]()
�⣺����![]() ���������壬��
���������壬��![]() ����ԭʽ
����ԭʽ![]() ��
��
�ٽ���![]() ����ԭ����ԭʽ
����ԭ����ԭʽ![]() ��
��
��������Ŀ�õ����ǣ�����˼�룬������˼��������ѧ�����г��õ�һ��˼�뷽����
������������ʽ�ֽ�ķ������ṫ��ʽ����ʽ�������еĶ���ʽֻ������һ�ַ������ֽ⣬����![]() ������ϸ�Ĺ۲�ͻᷢ�֣�ǰ��������Էֽ⣬������Ҳ���Էֽ⣬�ֱ�ֽ����������ʽ�Ϳ��������ֽ�����
������ϸ�Ĺ۲�ͻᷢ�֣�ǰ��������Էֽ⣬������Ҳ���Էֽ⣬�ֱ�ֽ����������ʽ�Ϳ��������ֽ�����
���̣�![]()
![]() ��
��
���ַ����з���ֽⷨ�����ڳ�������Ķ���ʽ�����������ַ�����
����������ѧ˼�뷽������������⣺
��1���ֽ���ʽ��![]()
��2���ֽ���ʽ��![]()
��3���ֽ���ʽ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90�㣬��B��30�㣬AB��4![]() cm������P�ӵ�B����������BC������2cm/s���ٶ��˶������˶���ʱ��Ϊt�룬��t��_____��ʱ����ABPΪֱ�������Σ�
cm������P�ӵ�B����������BC������2cm/s���ٶ��˶������˶���ʱ��Ϊt�룬��t��_____��ʱ����ABPΪֱ�������Σ�
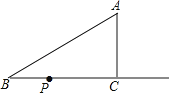
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x1��x2�Ƿ���x2����2k��1��x+��k2+3k+5��=0������ʵ��������x12+x22=39����k��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵ���ֱ�������Σ��ҡ�ACB��90�㣬��D��AB���ϵ�һ�㣨��D����A��B�غϣ�������CD������C��CE��CD����CE��CD������DE��AE��
��1����֤����CBD�ա�CAE��
��2����AD��4��BD��8����DE�ij���
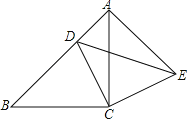
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������һö�ʵؾ��ȵ�Ӳ�ҡ�����ʱ������˵����ȷ������ ��
A. �����������������ӣ����泯�ϵ�Ƶ��Խ��ԽС
B. �������Ĵ����ܴ�ʱ�����泯�ϵĴ���һ��ռ������������![]()
C. ��ͬ���������飬���泯�ϵ�Ƶ�ʿ��ܻ��ͬ
D. ��������11��Ӳ�Ҷ������泯�ϣ���12�������������泯�ϵĸ���С��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�E��BC����һ�㣬����AE���ӳ�CB����F��ʹ![]() ������F��
������F��![]() �ڵ�H������FH�ֱ�AB��CD�ڵ�M��N�����Խ���AC�ڵ�P������AF��
�ڵ�H������FH�ֱ�AB��CD�ڵ�M��N�����Խ���AC�ڵ�P������AF��
![]() �����ⲹȫͼ�Σ�
�����ⲹȫͼ�Σ�
![]() ��֤��
��֤��![]() ��
��
![]() �ж��߶�FM��PN��������ϵ��������֤����
�ж��߶�FM��PN��������ϵ��������֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��б��AF���¶�Ϊ5��12��б��AF��һ����ˮƽ�洹ֱ�Ĵ���BD�����������£���б���ϵ�Ӱ��BC=6.5�ף���ʱ������ˮƽ��ǡ�ó�30��ǣ������BD�ĸߣ��������ȷ��0.1�ף��ο�����![]() ��1.414��
��1.414��![]() ��1.732��
��1.732��
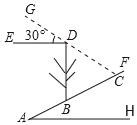
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com