练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在正方形ABCD中，E是BC边上一点，连接AE，延长CB至点F，使，过点F作于点H，射线FH分别交AB、CD于点M、N，交对角线AC于点P，连接AF．

    依题意补全图形；

    求证：；

    判断线段FM与PN的数量关系，并加以证明．

    【答案】（1）详见解析；（2）详见解析；（3）FM=PN，理由详见解析.

    【解析】

    依题意补全图形即可；利用三角形的内角和定理判断出，由等腰三角形的性质证得，再用正方形的性质得出，即可得出结论； 如图1，过B作交CD于点Q，构造出≌，进而判断出，再判断出，，即可得出结论．

    补全图形，如图所示：

    证明正方形ABCD，

    ，，

    ．

    ．

    ．

    ，

    ，．

    ．

    ；

    ．

    证明：如图1，过B作交CD于点Q，

    ，．

    正方形ABCD，

    ，，

    ．

    ≌．

    ．

    ．

    ，

    ．

    ，

    ．

    ．

    ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】“垃圾不落地，城市更美丽”．某中学为了了解七年级学生对这一倡议的落实情况，学校安排政教处在七年级学生中随机抽取了部分学生，并针对学生“是否随手丢垃圾”这一情况进行了问卷调查，统计结果为：A为从不随手丢垃圾；B为偶尔随手丢垃圾；C为经常随手丢垃圾三项．要求每位被调查的学生必须从以上三项中选一项且只能选一项．现将调查结果绘制成以下来不辜负不完整的统计图．

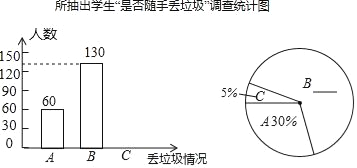
    请你根据以上信息，解答下列问题：

    (1)补全上面的条形统计图和扇形统计图；

    (2)所抽取学生“是否随手丢垃圾”情况的众数是　 　；

    (3)若该校七年级共有1500名学生，请你估计该年级学生中“经常随手丢垃圾”的学生约有多少人？谈谈你的看法？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司销售部有营销员15人，销售部为了制定关于某种商品的每位营销员的个人月销售定额，统计了这15人某月关于此商品的个人月销售量（单位：件）如下：

    个人月销售量

    1800

    510

    250

    210

    150

    120

    营销员人数

    1

    1

    3

    5

    3

    2

    （1）求这15位营销员该月关于此商品的个人月销售量的平均数，并直接写出这组数据的中位数和众数；

    （2）假设该销售部负责人把每位营销员关于此商品的个人月销售定额确定为320件，你认为对多数营销员是否合理？并在（1）的基础上说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在数学课上，老师提出一个问题“用直尺和圆规作一个矩形”．

    小华的做法如下：

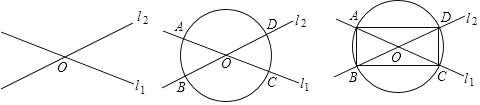
    如图1，任取一点O，过点O作直线l1，l2；如图2，以O为圆心，任意长为半径作圆，与直线l1，l2分别相交于点A、C，B、D；如图3，连接AB、BC、CD、DA四边形ABCD即为所求作的矩形．

    老师说：“小华的作法正确”．

    请回答：小华的作图依据是______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

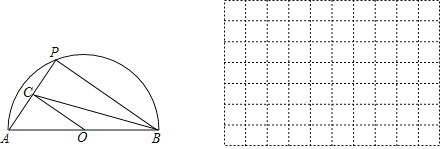
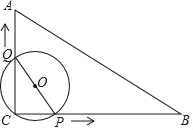
    【题目】如图，P是半圆弧上一动点，连接PA、PB，过圆心O作交PA于点C，连接已知，设O，C两点间的距离为xcm，B，C两点间的距离为ycm．

    小东根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行探究．

    下面是小东的探究过程，请补充完整：

    通过取点、画图、测量，得到了x与y的几组值，如下表：

    0

    1

    2

    3

    3

    6

    说明：补全表格时相关数据保留一位小数

    建立直角坐标系，描出以补全后的表中各对应值为坐标的点，画出该函数的图象；

    结合画出的函数图象，解决问题：直接写出周长C的取值范围是______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，ABCD的周长为36，对角线AC、BD相交于点O，点E是CD的中点，BD=12，则△DOE的周长为（　　）

    A. 15 B. 18 C. 21 D. 24

    查看答案和解析>>

    科目：初中数学 来源： 题型：

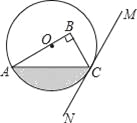
    【题目】如图，在Rt△ABC中，∠B=90°，点O在边AB上，以点O为圆心，OA为半径的圆经过点C，过点C作直线MN，使∠BCM=2∠A．

    （1）判断直线MN与⊙O的位置关系，并说明理由；

    （2）若OA=4，∠BCM=60°，求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料，回答问题：

    小聪学完了“锐角三角函数”的相关知识后，通过研究发现：如图1，在Rt△ABC中，如果∠C=90°，∠=30°，BC═a=1，AC=b=，AB=c=2，那么==2．通过上网查阅资料，他又知“sin90°=1”，因此他得到“在含30°角的直角三角形中，存在着==的关系．

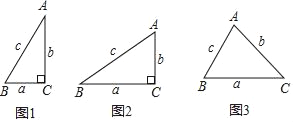
    这个关系对于一般三角形还适用吗？为此他做了如下的探究：

    （1）如图2，在R△ABC中，∠C=90°，BC=a，AC=b，AB=C，请判断此时“==”的关系是否成立？答：　 　

    （2）完成上述探究后，他又想“对于任意的锐角△ABC，上述关系还成立吗？”因此他又继续进行了如下的探究：

    如图3，在锐角△ABC中，BC=a，AC=b，AB=c，请判断此时“ ==”的关系是否成立？并证明你的判断．（提示：过点C作CD⊥AB于D，过点A作AH⊥BC，再结合定义或其它方法证明）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，AC=2cm，AB=4cm，动点P从点C出发，在BC边上以每秒cm的速度向点B匀速运动，同时动点Q也从点C出发，沿C→A→B以每秒4cm的速度匀速运动，运动时间为t秒，连接PQ，以PQ为直径作⊙O．

    （1）当时，求△PCQ的面积；

    （2）设⊙O的面积为s，求s与t的函数关系式；

    （3）当点Q在AB上运动时，⊙O与Rt△ABC的一边相切，求t的值．

    查看答案和解析>>

    同步练习册答案