【题目】如图，
是
的内切圆，点
、
分别为
，
上的点，且
为的切线，若的周长为
，
边的长为
．则
的周长为（ ）
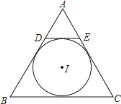
A. 15 B. 7.5 C. 10 D. 9
【答案】C
【解析】
根据切线长定理可以证得：BF+CH=BG+CG=BC，DE=DR+ER=DF+EH，根据△ADE的周长=AD+AE+DE=AD+AE+DF+EH=AF+AH=△ABC的周长-（BF+CH）=△ABC的周长-BC即可求解.
解：∵⊙I是△ABC的内切圆，设与AB，BC，AC的切点分别为：F，G，H，
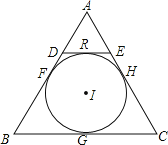
∴BF=BG，CG=CH，DR=DF，ER=EH,
∴BF+CH=BG+CG=BC=5，
DE=DR+ER=DF+EH，
∴△ADE的周长=AD+AE+DE=AD+AE+DF+EH=AF+AH=△ABC的周长-BC-（BF+CH）=△ABC的周长-2BC=20-2×5=10．
故选：C.
科目：初中数学 来源： 题型：
【题目】在做“抛掷一枚质地均匀的硬币”试验时，下列说法正确的是（ ）
A. 随着抛掷次数的增加，正面朝上的频率越来越小
B. 当抛掷的次数很大时，正面朝上的次数一定占总抛掷次数的
C. 不同次数的试验，正面朝上的频率可能会不相同
D. 连续抛掷11次硬币都是正面朝上，第12次抛掷出现正面朝上的概率小于
查看答案和解析>>
科目：初中数学 来源： 题型：
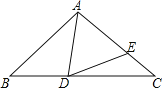
【题目】如图，已知在△ABC中，AB＝AC，D是BC边上任意一点，E在AC边上，且AD＝AE．
（1）若∠BAD＝40°，求∠EDC的度数；
（2）若∠EDC＝15°，求∠BAD的度数；
（3）根据上述两小题的答案，试探索∠EDC与∠BAD的关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
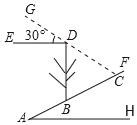
【题目】如图，斜坡AF的坡度为5：12，斜坡AF上一棵与水平面垂直的大树BD在阳光照射下，在斜坡上的影长BC=6.5米，此时光线与水平线恰好成30°角，求大树BD的高．（结果精确的0.1米，参考数据
≈1.414，
≈1.732）
查看答案和解析>>
科目：初中数学 来源： 题型：
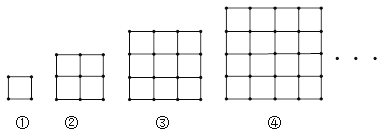
【题目】如图，图①由4根火柴棍围成；图②由12根火柴棍围成；图③由24根火柴棍围成；…按此规律，则第⑥个图形由（ ）根火柴棍围成.
A. 60 B. 72 C. 84 D. 112
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知平行四边形ABCD中，G为BC中点，点E在AD边上，且∠1=∠2．
(1)求证：E是AD中点；
(2)若F为CD延长线上一点，连接BF，且满足∠3=∠2，求证：CD=BF+DF．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】鼎丰超市以固定进价一次性购进保温杯若干个，11月份按一定售价销售，销售额为1800元，为扩大销量，减少库存，12月份在11月份售价基础上打9折销售，结果销售量增加50个，销售额增加630元．
（1）求鼎丰超市11月份这种保温杯的售价是多少元？
（2）如果鼎丰超市11月份销售这种保温杯的利润为600元，那么该鼎丰超市12月份销售这种保温杯的利润是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y=ax2+bx（a≠0）过点E（10，0），矩形ABCD的边AB在线段OE上（点A在点B的左边），点C，D在抛物线上．设A（t，0），当t=2时，AD=4．
（1）求抛物线的函数表达式．
（2）当t为何值时，矩形ABCD的周长有最大值？最大值是多少？
（3）保持t=2时的矩形ABCD不动，向右平移抛物线．当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形的面积时，求抛物线平移的距离．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
