
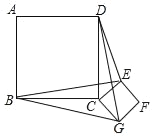
【题目】如图,正方形ABCD和正方形CEFG的边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论是( )
A. ①B. ②C. ①②D. ①②③
【答案】D
【解析】
根据正方形的性质易证△DCG≌△BEC,即可证得BE=DG,BE⊥DG,由此判断①②正确;根据勾股定理可得BD2=DM2+BM2,EG2=ME2+MG2,则BD2+EG2=DM2+BM2+ME2+MG2,可得BD2+EG2=BG2+DE2.再把a,b代入即可证得③正确.
如图:连接BD,EG,BE,DG的交点为M
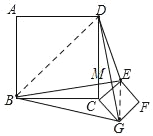
∵四边形ABCD,四边形CEFG 为正方形
∴BC=DC,CG=CE,∠BCD=∠ECG,
∴∠BCE=∠DCG,且BC=DC,CG=CE,
∴△BCE≌△DCG,
∴DG=BE,∠CBE=∠CDE,
∵∠DBE+∠EBC+∠BDC+∠BCD=180°,
∴∠DBE+∠EBC+∠BDC=90°,
∵∠DBE+∠CDE+∠BDC+∠BMD=180°,
∴∠DCB=∠DMB=90°,
∴BE⊥DG故①②正确.
∵BE⊥DG,
∴BD2=DM2+BM2,EG2=ME2+MG2,
∴BD2+EG2=DM2+BM2+ME2+MG2,
∴BD2+EG2=BG2+DE2.
∴AB2+AD2+EC2+CG2=BG2+DE2.
∴2a2+2b2=BG2+DE2,故③正确
故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,把平面内一条数轴x绕点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:已知点P是平面斜坐标系中任意一点,过点P作y轴的平行线交x轴于点A,过点P作x轴的平行线交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对(a,b)为点P的斜坐标.在平面斜坐标系中,若θ=45°,点P的斜坐标为(1,2![]() ),点G的斜坐标为(7,﹣2
),点G的斜坐标为(7,﹣2![]() ),连接PG,则线段PG的长度是_____.
),连接PG,则线段PG的长度是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中“优秀”所对应的扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,回答问题:
小聪学完了“锐角三角函数”的相关知识后,通过研究发现:如图1,在Rt△ABC中,如果∠C=90°,∠=30°,BC═a=1,AC=b=![]() ,AB=c=2,那么
,AB=c=2,那么![]() =
=![]() =2.通过上网查阅资料,他又知“sin90°=1”,因此他得到“在含30°角的直角三角形中,存在着
=2.通过上网查阅资料,他又知“sin90°=1”,因此他得到“在含30°角的直角三角形中,存在着![]() =
=![]() =
=![]() 的关系.
的关系.
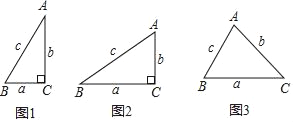
这个关系对于一般三角形还适用吗?为此他做了如下的探究:
(1)如图2,在R△ABC中,∠C=90°,BC=a,AC=b,AB=C,请判断此时“![]() =
=![]() =
=![]() ”的关系是否成立?答:
”的关系是否成立?答:
(2)完成上述探究后,他又想“对于任意的锐角△ABC,上述关系还成立吗?”因此他又继续进行了如下的探究:
如图3,在锐角△ABC中,BC=a,AC=b,AB=c,请判断此时“![]() =
=![]() =
=![]() ”的关系是否成立?并证明你的判断.(提示:过点C作CD⊥AB于D,过点A作AH⊥BC,再结合定义或其它方法证明).
”的关系是否成立?并证明你的判断.(提示:过点C作CD⊥AB于D,过点A作AH⊥BC,再结合定义或其它方法证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以水![]() 润
润![]() 城,打造
城,打造![]() 四河一库
四河一库![]() 生态水系工程,是巩义坚持不懈推进文明创建与百城提质深度融合的缩影,伊洛河畔正是此项目中的一段.如今,伊洛河畔需要铺设一条长为
生态水系工程,是巩义坚持不懈推进文明创建与百城提质深度融合的缩影,伊洛河畔正是此项目中的一段.如今,伊洛河畔需要铺设一条长为![]() 米的管道,决定由甲、乙两个工程队来完成.已知甲工程队比乙工程队每天能多铺设
米的管道,决定由甲、乙两个工程队来完成.已知甲工程队比乙工程队每天能多铺设![]() 米,且甲工程队铺设
米,且甲工程队铺设![]() 米所用的天数与乙工程队铺设
米所用的天数与乙工程队铺设![]() 米所用的天数相同.(完成任务的工期为整数)
米所用的天数相同.(完成任务的工期为整数)
(1)甲、乙工程队每天各能铺设多少米?
(2)如果要求完成该项管道铺设任务的工期不超过![]() 天,那么为两工程队分配工程量的方案有几种?请你帮助设计出来(工程队分配工程量为整百数)
天,那么为两工程队分配工程量的方案有几种?请你帮助设计出来(工程队分配工程量为整百数)
查看答案和解析>>
科目:初中数学 来源: 题型:
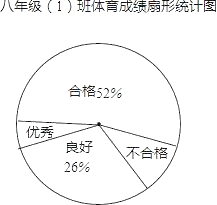
【题目】某校对九年级(1)班全体学生进行体育测试,测试成绩分为优秀、良好、合格和不合格四个等级,根据测试成绩绘制的不完整统计图表如下:
九年级(1)班体育成绩频数分布表:
等级 | 分值 | 频数 |
优秀 | 90﹣100分 | |
良好 | 75﹣89分 | 13 |
合格 | 60﹣74分 | |
不合格 | 0﹣59分 | 9 |
根据统计图表给出的信息,解答下列问题:
(1)九年级(1)班共有多少名学生?
(2)体育成绩为优秀的频数是 ,合格的频数为 ;
(3)若对该班体育成绩达到优秀程度的3个男生和2个女生中随机抽取2人参加学校体育竞赛,恰好抽到1个男生和1个女生的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com