
【题目】已知⊙O的半径为1,弦AB=![]() ,弦AC=
,弦AC=![]() ,则∠BAC的度数为___.
,则∠BAC的度数为___.
【答案】15°或75°
【解析】
连接OA,过O作OE⊥AC于E,OF⊥AB于F,根据垂径定理求出AE、FA值,根据解直角三角形的知识求出∠OAB和∠OAC,然后分两种情况求出∠BAC即可.
解:有两种情况:
①如图1所示:
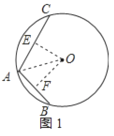
连接OA,过O作OE⊥AC于E,OF⊥AB于F,
∴∠OEA=∠OFA=90°,
由垂径定理得:AE=CE=![]() ,AF=BF=
,AF=BF=![]()
cos∠OAE=![]() =
=![]() ,cos∠OAF=
,cos∠OAF=![]() =
=![]() ,
,
∴∠OAE=30°,∠OAF=45°,
∴∠BAC=30°+45°=75°;
②如图2所示
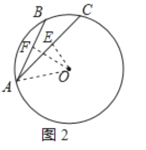
连接OA,过O作OE⊥AC于E,OF⊥AB于F,
∴∠OEA=∠OFA=90°,
由垂径定理得:AE=CE=![]() ,AF=BF=
,AF=BF=![]() ,
,
cos∠OAE═![]() =
=![]() ,cos∠OAF=
,cos∠OAF=![]() =
=![]() ,
,
∴∠OAE=30°,∠OAF=45°,
∴∠BAC=45°30°=15°;
故答案为:75°或15°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 。
。
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为
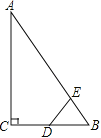
A、2 B、2.5或3.5 C、3.5或4.5 D、2或3.5或4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
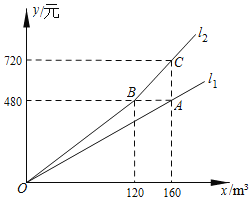
【题目】某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中![]() 、
、![]() 分别表示去年、今年水费
分别表示去年、今年水费![]() (元)与用水量
(元)与用水量![]() (
(![]() )之间的关系.小雨家去年用水量为150
)之间的关系.小雨家去年用水量为150![]() ,若今年用水量与去年相同,水费将比去年多_____元.
,若今年用水量与去年相同,水费将比去年多_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
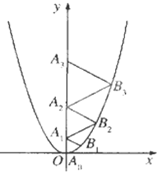
【题目】二次函数![]() 的图象如图所示,点
的图象如图所示,点![]() 位于坐标原点O,
位于坐标原点O, ![]() 在y轴的正半轴上,点
在y轴的正半轴上,点![]() 在二次函数
在二次函数![]() 第一象限的图象上,若△
第一象限的图象上,若△![]() ,△
,△![]() ,△
,△![]() …,都为等边三角形,则点
…,都为等边三角形,则点![]() 的坐标为_____
的坐标为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相交于点D,且∠A=2∠DCB,连接CD.

(1)求证:AB是⊙O的切线;
(2)若BE=OE=2,求图中阴影部分的面积(结果保留![]() 和根号).
和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔(J.Nplcr,1550﹣1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707﹣1783年)才发现指数与对数之间的联系.
对数的定义:一般地,若![]() (
(![]() 且
且![]() ),那么
),那么![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记作
的对数,记作![]() ,比如指数式
,比如指数式![]() 可以转化为对数式
可以转化为对数式![]() ,对数式
,对数式![]() ,可以转化为指数式
,可以转化为指数式![]() .
.
我们根据对数的定义可得到对数的一个性质:
![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() ),理由如下:
),理由如下:
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,由对数的定义得
,由对数的定义得![]()
又∵![]()
∴![]()
根据阅读材料,解决以下问题:
(1)将指数式![]() 转化为对数式________;
转化为对数式________;
(2)求证:![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )
)
(3)拓展运用:计算![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2cm的等边△ABC的边BC在直线l上,两条距离为1cm的平行直线a和b垂直于直线l,直线a、b同时向右移动(直线a的起始位置在B点),运动速度为1cm/s,直到直线a到达C点时停止.在a、b向右移动的过程中,记△ABC夹在a和b之间的部分的面积为S,求S与t的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
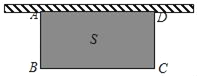
【题目】如图.利用一面墙(墙的长度不限),用20m的篱笆围成一个矩形场地ABCD.设矩形与墙垂直的一边AB=xm,矩形的面积为Sm2.
(1)用含x的式子表示S;
(2)若面积S=48m2,求AB的长;
(3)能围成S=60m2的矩形吗?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com