
【题目】我们已经知道,乘法公式可以用一些硬纸片拼成的图形面积来解释其正确性,实际上还有很多代数恒等式也可用这种形式说明其正确性.例如图1可以用来解释:2a(a+b)=2a2+2ab.
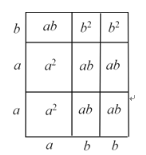
(1)试写出图2所表示的代数恒等式: ;
(2)试在图3的方框内画出一个平面图形,使它的面积能表示: (2a+b)(a+2b)=2a2+5ab+2b2.

【答案】(1)(a+b)(a+2b)= a2+3ab+2b2;(2)见解析
【解析】
(1)根据图2中长方形面积的两种求法即可得出结论;
(2)先画一个长方形,将长方形的一边分成一条长为a,两条长为b的线段,然后从这三条线段的端点处在长方形的内部画竖线,再将长方形的另一边分成两条长为a,一条长为b的线段,然后从这三条线段的端点处在长方形的内部画横线即可.
解:(1)由图2可知:图中长方形的面积等于长×宽,也等于这些小长方形的面积之和
(a+b)(a+2b)= a2+ab+ab +ab +b2+b2= a2+3ab+2b2
故答案为:(a+b)(a+2b)= a2+3ab+2b2;
(2)先画一个长方形,将长方形的一边分成一条长为a,两条长为b的线段,然后从这三条线段的端点处在长方形的内部画竖线,再将长方形的另一边分成两条长为a,一条长为b的线段,然后从这三条线段的端点处在长方形的内部画横线,如下图所示,该平面图形即为所求.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:对于一些次数较高或者是比较复杂的式子进行因式分解时,换元法是一种常用的方法,下面是某同学用换元法对多项式![]() 进行因式分解的过程.
进行因式分解的过程.
解:设![]()
原式![]() (第一步)
(第一步)
![]() (第二步)
(第二步)
![]() (第三步)
(第三步)
![]() (第四步)
(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的__________(填代号).
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)按照“因式分解,必须进行到每一个多项式因式都不能再分解为止”的要求,该多项式分解因式的最后结果为______________.
(3)请你模仿以上方法对多项式![]() 进行因式分解.
进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是-2,点B的横坐标是3,则以下结论:
①抛物线y=ax2(a≠0)的图象的顶点一定是原点;
②x>0时,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)的函数值都随着x的增大而增大;
③AB的长度可以等于5;
④△OAB有可能成为等边三角形;
⑤当-3<x<2时,ax2+kx<b,
其中正确的结论是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划选购![]() 、
、![]() 两种图书.已知
两种图书.已知![]() 种图书每本价格是
种图书每本价格是![]() 种图书每本价格的2.5倍,用1200元单独购买
种图书每本价格的2.5倍,用1200元单独购买![]() 种图书比用1500元单独购买
种图书比用1500元单独购买![]() 种图书要少25本.
种图书要少25本.
(1)![]() 、
、![]() 两种图书每本价格分别为多少元?
两种图书每本价格分别为多少元?
(2)如果该学校计划购买![]() 种图书的本数比购买
种图书的本数比购买![]() 种图书本数的2倍多8本,且用于购买
种图书本数的2倍多8本,且用于购买![]() 、
、![]() 两种图书的总经费不超过1164元,那么该学校最多可以购买多少本
两种图书的总经费不超过1164元,那么该学校最多可以购买多少本![]() 种图书?
种图书?
查看答案和解析>>
科目:初中数学 来源: 题型:
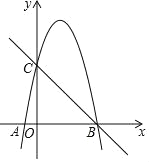
【题目】如图,抛物线y=﹣x2+4x+5与x轴,y轴分别交于A,B,C三点.
(1)请直接写出A,B,C三点坐标:A(_____,_____)、B(_____,______)、C(______,______)
(2)若⊙M过A、B、C三点,求圆心M的坐标,并求⊙M的面积;
(3)在(2)的条件下,在抛物线上是否存在点N,使得由A,C,M,N四点构成的四边形为平行四边形?若存在,请求出点N的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是高线,
是高线,![]() ,
,![]() ,
,
(1)用直尺与圆规作三角形内角![]() 的平分线
的平分线![]() (不写作法,保留作图痕迹).
(不写作法,保留作图痕迹).
(2)在(1)的前提下,判断①![]() ,②
,②![]() 中哪一个正确?并说明理由.
中哪一个正确?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.

(1)求证:△DEF是等腰三角形;
(2)当∠A=36°时,求∠DEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从一副52张(没有大小王)的扑克牌中,每次抽出1张,然后放回洗匀再抽,在试验中得到下表中部分数据:
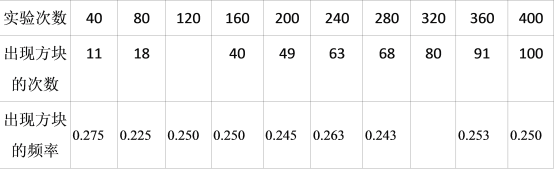
(1)将数据表补充完整;
(2)从上表中可以估计出现方块的概率是________(精确到0.01);
(3)从这副扑克牌中取出两组牌,分别是方块1,2,3和红桃1,2,3,将它们背面朝上分别重新洗牌后,从两组牌中各摸出一张,若摸出的两张牌的牌面数字之和等于3,则甲方赢;若摸出的两张牌的牌面数字之和等于4,则乙方赢.你认为这个游戏对双方是公平的吗?若不是,有利于谁?请你用概率知识(列表法或画树状图法)加以分析说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.



(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
② 设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com