
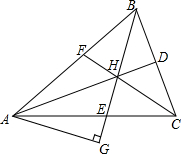
 如图,在△ABC中,角平分线AD,BE,CF相交于点H,过A点作AG⊥BE,垂足为G,那么∠HAG=$\frac{1}{2}$∠ACB吗?为什么?
如图,在△ABC中,角平分线AD,BE,CF相交于点H,过A点作AG⊥BE,垂足为G,那么∠HAG=$\frac{1}{2}$∠ACB吗?为什么? 分析 由题意可得:∠BAD+∠CAD+∠EAG+∠ABG=90°,又∠ABG+∠BAD+∠ACF=90°,两者联立得出∠BAD+∠CAD+∠EAG+∠ABG=∠ABG+∠BAD+∠ACF,进一步整理得出答案即可.
解答 解:∵AG⊥BE,
∴∠AGA=90°,
∴∠BAD+∠CAD+∠EAG+∠ABG=90°,
∵AD,BE,CF是△ABC的角平分线,
∴∠ABG=$\frac{1}{2}$∠ABC,∠BAD=$\frac{1}{2}$∠BAC,∠ACF=$\frac{1}{2}$∠ACB,
∴∠ABG+∠BAD+∠ACF=$\frac{1}{2}$(∠ABC+$\frac{1}{2}$∠BAC+∠ACB)=90°,
∴∠BAD+∠CAD+∠EAG+∠ABG=∠ABG+∠BAD+∠ACF,
即∠CAD+∠EAG=∠ACF,
∴∠HAG=$\frac{1}{2}$∠ACB.
点评 此题考查三角形的内角和定理,角平分线的性质,掌握三角形的内角和180°是解决问题的关键.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a+b}{{{a^2}+{b^2}}}$ | B. | $\frac{a}{{{a^2}-3a}}$ | C. | $\frac{2a}{{3{a^2}b}}$ | D. | $\frac{{{a^2}-ab}}{{{a^2}-{b^2}}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{x}^{2}}$ | B. | $\frac{x}{\sqrt{3}}$ | C. | $\sqrt{8}$ | D. | $\frac{\sqrt{2x}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com