
| A. | $\frac{a+b}{{{a^2}+{b^2}}}$ | B. | $\frac{a}{{{a^2}-3a}}$ | C. | $\frac{2a}{{3{a^2}b}}$ | D. | $\frac{{{a^2}-ab}}{{{a^2}-{b^2}}}$ |
分析 利用最简分式的定义:一个分式的分子与分母没有公因式时,叫最简分式,可得结果.
解答 解:A.分子分母不能分解因式,也没有公因式,是最简分式;
B.$\frac{a}{{a}^{2}-3a}$=$\frac{a}{a(a-3)}$=$\frac{1}{a-3}$,所以不是最简分式;
C.$\frac{2a}{{3a}^{2}b}$=$\frac{2}{3ab}$,所以不是最简分式;
D.$\frac{{a}^{2}-ab}{{a}^{2}{-b}^{2}}$=$\frac{a(a-b)}{(a+b)(a-b)}$=$\frac{a}{a+b}$,所以不是最简分式;
故选A.
点评 本题主要考查了最简分式,先将分子分母因式分解是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
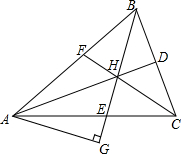 如图,在△ABC中,角平分线AD,BE,CF相交于点H,过A点作AG⊥BE,垂足为G,那么∠HAG=$\frac{1}{2}$∠ACB吗?为什么?
如图,在△ABC中,角平分线AD,BE,CF相交于点H,过A点作AG⊥BE,垂足为G,那么∠HAG=$\frac{1}{2}$∠ACB吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0<x≤1 | B. | x≥1 | C. | x>0 | D. | 0≤x≤1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com