
分析 (1)去括号、移项、合并同类项、系数化成1即可求解;
(2)首先对二次根式进行化简,然后利用乘法法则计算即可求解;
(3)利用求根公式即可直接求解.
解答 解:(1)去括号,得3x-2-4x≥1
移项、合并同类项,得-x≥3
系数化成1得x≤-3;
(2)原式=$(\sqrt{3}+2\sqrt{6}-2\sqrt{6})•2\sqrt{3}$
=$\sqrt{3}•2\sqrt{3}$
=6;
(3)∵a=2,b=-4,c=-1,
△=16+8=24,
∴x=$\frac{4±2\sqrt{6}}{4}$=$\frac{2±\sqrt{6}}{2}$.
∴原方程有解为x1=$\frac{2+\sqrt{6}}{2}$,x2=$\frac{2-\sqrt{6}}{2}$.
点评 本题考查的是二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:初中数学 来源: 题型:选择题
| A. | 2<m<3 | B. | 3<m<4 | C. | -3<m<-2 | D. | -4<m<-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
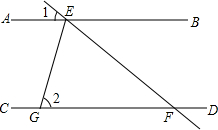 如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,EG平分∠AEF交CD于点G.若∠1=36°,则∠2的大小是( )
如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,EG平分∠AEF交CD于点G.若∠1=36°,则∠2的大小是( )| A. | 68° | B. | 70° | C. | 71° | D. | 72° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
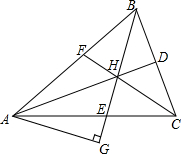 如图,在△ABC中,角平分线AD,BE,CF相交于点H,过A点作AG⊥BE,垂足为G,那么∠HAG=$\frac{1}{2}$∠ACB吗?为什么?
如图,在△ABC中,角平分线AD,BE,CF相交于点H,过A点作AG⊥BE,垂足为G,那么∠HAG=$\frac{1}{2}$∠ACB吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
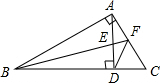 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D点,∠ABC的平分线分别交AD、AC于E、F两点,连结DF,下列结论:①△AEF为等腰三角形;②△FAD为等腰三角形;③△BDE∽△BAF;④△ABE∽△CBF,其中正确的有( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D点,∠ABC的平分线分别交AD、AC于E、F两点,连结DF,下列结论:①△AEF为等腰三角形;②△FAD为等腰三角形;③△BDE∽△BAF;④△ABE∽△CBF,其中正确的有( )| A. | ①②④ | B. | ①③④ | C. | ②④ | D. | ①③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com