
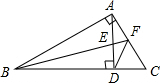
 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D点,∠ABC的平分线分别交AD、AC于E、F两点,连结DF,下列结论:①△AEF为等腰三角形;②△FAD为等腰三角形;③△BDE∽△BAF;④△ABE∽△CBF,其中正确的有( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D点,∠ABC的平分线分别交AD、AC于E、F两点,连结DF,下列结论:①△AEF为等腰三角形;②△FAD为等腰三角形;③△BDE∽△BAF;④△ABE∽△CBF,其中正确的有( )| A. | ①②④ | B. | ①③④ | C. | ②④ | D. | ①③ |
分析 利用等角的余角相等得∠BAD=∠C,再根据三角形外角性质得∠AEF=∠ABE+∠BAE,∠AFE=∠FBC+∠C,则得到∠AEF=∠AFE,可判断△AEF为等腰三角形,于是可对①进行判断;根据直角三角形斜边上的中线等于斜边的一半对②进行判断;根据有两组角对应相等的两个三角形相似对③④进行判断.
解答 解:∵∠BAC=90°,AD⊥BC,
∴∠BAD=∠C,
∵∠AEF=∠ABE+∠BAE,∠AFE=∠FBC+∠C,
∵BF平分∠ABC,
∴∠AEF=∠AFE,
∴△AEF为等腰三角形,所以①正确;
∵BF为角平分线,F点不能确定为AC的中点,
∴FA和FD不能确定相等,所以②错误;
∵∠ABF=∠DBE,∠BAF=∠BDE,
∴△BDE∽△BAF,所以③正确;
∵∠AEF=∠AFE,
∴∠AEB=∠BFC,
∵∠ABE=∠CBF,
∴△ABE∽△CBF,所以④正确.
故选B.
点评 本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了等腰三角形的判定.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
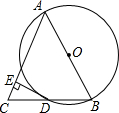 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,垂足为E.
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
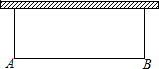 如图中有一面围墙(可利用的最大长度为100m),现打算沿围墙围成一个面积为120m2的长方形花圃.设花圃的一边AB=xm,另一边为ym,求y关于x的函数表达式,并指出其中自变量的取值范围.
如图中有一面围墙(可利用的最大长度为100m),现打算沿围墙围成一个面积为120m2的长方形花圃.设花圃的一边AB=xm,另一边为ym,求y关于x的函数表达式,并指出其中自变量的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{x}^{2}}$ | B. | $\frac{x}{\sqrt{3}}$ | C. | $\sqrt{8}$ | D. | $\frac{\sqrt{2x}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com