
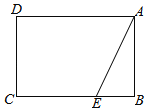
【题目】已知矩形ABCD中,AB=2,BC=m,点E是边BC上一点,BE=1,连接AE.
(1)沿AE翻折△ABE使点B落在点F处,
①连接CF,若CF∥AE,求m的值;
②连接DF,若![]() ≤DF≤
≤DF≤![]() ,求m的取值范围.
,求m的取值范围.
(2)△ABE绕点A顺时针旋转得△AB1E1,点E1落在边AD上时旋转停止.若点B1落在矩形对角线AC上,且点B1到AD的距离小于![]() 时,求m的取值范围.
时,求m的取值范围.
【答案】(1)①2;②1≤m![]() ;(2)
;(2)![]() <m≤4.
<m≤4.
【解析】
(1)①画出图形,由CF∥AE可得内错角和同位角相等,由翻折有对应角相等,等量代换后出现等腰三角形,即求出m的值.
②由于△ABE的形状大小是固定的,其翻折图形也固定,故可求点F到AD的距离FG与AG的长度,根据△DFG是直角三角形即可利用勾股定理用含m的式子表示DF2的长度,此时可把DF2看作是m的二次函数,根据二次函数图象的性质和DF2的范围,确定自变量m的范围.
(2)根据点B1在AC上,利用内错角相等即三角函数相等可用含m的式子表示B1到AC的距离B1M,即求出m的最小值.又画图可知,当点E1落在AD上时,m最大,画出图形,利用∠ACB=∠B1AE1即三角函数相等即求出m的值.
解:(1)①如图1,∵CF∥AE
∴∠FCE=∠AEB,∠CFE=∠AEF
∵△ABE翻折得到△AFE
∴EF=BE=1,∠AEF=∠AEB
∴∠FCE=∠CFE
∴CE=EF=1
∴m=BC=BE+CE=2
∴m的值是2.
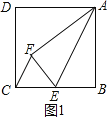
②如图2,过点F作GH⊥AD于点G,交BC于点H
∴GH⊥BC
∴∠AGF=∠FHE=90°
∵四边形ABCD是矩形
∴∠BAD=∠B=90°
∴四边形ABHG是矩形
∴GH=AB=2,AG=BH
∵△ABE翻折得到△AFE
∴EF=BE=1,AF=AB=2,∠AFE=∠B=90°
∴∠AFG+∠EFH=∠AFG+∠FAG=90°
∴∠EFH=∠FAG
∴△EFH∽△FAG
∴![]()
设EH=x,则AG=BH=x+1
∴FG=2EH=2x
∴FH=GH﹣FG=2﹣2x
∴![]()
解得:x=![]()
∴AG=![]() ,FG=
,FG=![]()
∵AD=BC=m
∴DG=|AD﹣AG|=|m﹣![]() |
|
∴DF2=DG2+FG2=(m﹣![]() )2+
)2+![]() 2≥
2≥![]() ,
,
即可把DF2看作关于m的二次函数,抛物线开口向上,最小值为![]() .
.
∵![]()
∴![]()
∵(m﹣![]() )2+
)2+![]() 2=
2=![]() 解得:m1=
解得:m1=![]() ,m2=1
,m2=1
∴根据二次函数图象可知,1≤m![]()
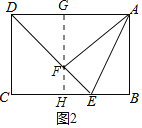
(2)如图3,过点B1作MN⊥AD于点M,交BC于点N
∴MN∥AB,MN=AB=2
∵AC=![]()
∴sin∠ACB=![]()
∵AD∥BC,点B1在AC上
∴∠MAB1=∠ACB
∴sin∠MAB1=![]()
∴![]()
∵点B1到AD的距离小于![]()
∴MB1=![]()
解得:![]()
∵m>0
∴m>![]()
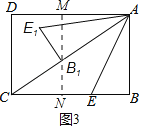
如图4,当E1落在边AD上,且B1在AC上时,m最大,
此时,∠ACB=∠B1AE1=∠BAE
∴tan∠ACB=tan∠BAE
∴![]()
∴m=BC=2AB=4
∴m的取值范围是![]() <m≤4
<m≤4



科目:初中数学 来源: 题型:
【题目】已知:如图,![]() 绕某点按一定方向旋转一定角度后得到
绕某点按一定方向旋转一定角度后得到![]() ,点A,B,C分别对应点A1,B1,C1 .
,点A,B,C分别对应点A1,B1,C1 .
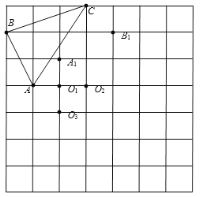
(1)根据点![]() 和
和![]() 的位置确定旋转中心是点______________.
的位置确定旋转中心是点______________.
(2)请在图中画出![]() ;
;
(3)请具体描述一下这个旋转:________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个如图所示的面积为300m2的长方形围栏,围栏总长50m,一边靠墙(墙长25m).
(1)求围栏的长和宽;
(2)能否围成面积为400m2的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)该抛物线的对称轴是![]() ________.
________.
(2)该抛物线与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,若此抛物线的对称轴上的点
,若此抛物线的对称轴上的点![]() 满足
满足![]() ,则点
,则点![]() 的纵坐标
的纵坐标![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
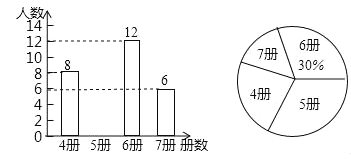
【题目】高尔基说:“书,是人类进步的阶梯.”阅读可以丰富知识、拓展视野、充实生活等诸多益处.为了解学生的课外阅读情况,某校随机抽查了部分学生阅读课外书册数的情况,并绘制出如下统计图,其中条形统计图因为破损丢失了阅读5册书数的数据.
(1)求条形图中丢失的数据,并写出阅读书册数的众数和中位数;
(2)根据随机抽查的这个结果,请估计该校1200名学生中课外阅读5册书的学生人数;
(3)若学校又补查了部分同学的课外阅读情况,得知这部分同学中课外阅读最少的是6册,将补查的情况与之前的数据合并后发现中位数并没有改变,试求最多补查了多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,D、E分别是AB,AC的中点,作∠B的角平分线
(1)如图1,若∠B的平分线恰好经过点E,猜想△ABC是怎样的特殊三角形,并说明理由;
(2)如图2,若∠B的平分线交线段DE于点F,已知AB=8,BC=10,求EF的长度;
(3)若∠B的平分线交直线DE于点F,直接写出AB、BC、EF三者之间的数量关系。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
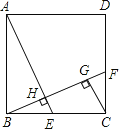
【题目】如图,在正方形ABCD中,E是BC上的一点,连结AE,作BF⊥AE,垂足为H,交CD于F,作CG∥AE,交BF于G.
求证:(1) CG=BH;(2)FC2=BF·GF;(3)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
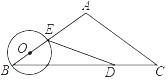
【题目】如图,等腰△ABC中,AB=AC=5cm,BC=8cm.动点D从点C出发,沿线段CB以2cm/s的速度向点B运动,同时动点O从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随时停止.设运动时间为t(s),以点O为圆心,OB长为半径的⊙O与BA交于另一点E,连接ED.当直线DE与⊙O相切时,t的取值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com