
����Ŀ��ij�����������������꼶������Ȥ���ã��Էḻѧ���������Ϊ���˽�ѧ�������֡��鷨�����ࡢ�滭���ĸ���ȤС���ϲ���������ȫ����������������飬�������ռ������ݻ�������������ͳ��ͼ����Ϣ���������������ͼ���ṩ����Ϣ�������������⣺
(1) �˴ι������� ��ͬѧ��
(2) ������ͼ������������������ͳ��ͼ�����ֲ��ֵ�Բ�ĽǵĶ����� ��
(3) ����������꼶����2 000��ѧ���μ���4��������ȤС�飬��ÿ����ʦ���ֻ�ܸ��������20��ѧ������滭��ȤС��������Ҫ����������ʦ��

���𰸡���1��300����2��ͼ��������� 96�㣻������20.
��������
(1)������������������ռ�ٷֱȿɵ�������;(2)���ݸ�������֮�͵��������������������,�ݴ˿ɲ�ȫ����ͼ,����360����������������ռ�����ɵ�;(3)���������������л滭������ռ����,�ٳ���20���ɵ�.
�⣺��1���˴ε����ѧ������Ϊ120��40%��300��������
��2�����ֵ�����Ϊ300����60+120+40����80��������
��ȫ����ͼ���£�
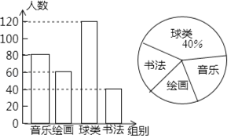
����ͳ��ͼ�����ֲ��ֵ�Բ�ĽǵĶ���Ϊ360���![]() ��96����
��96����
��3��60��300��2000��20��20�� ������20����ʦ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ҫ��Ӫһ�������е��ľߣ�����Ϊ20Ԫ�M���������η��֣������ۼ�Ϊ25Ԫ�M��ʱ��ÿ�����������250�������ۼ�ÿ����1Ԫ��ÿ����������ͼ���10����
��1��д���̳����������ľߣ�ÿ�����õ���������![]() ��Ԫ�������۵���
��Ԫ�������۵���![]() ��Ԫ��֮��ĺ�����ϵʽ��
��Ԫ��֮��ĺ�����ϵʽ��
��2�������۵���Ϊ����Ԫʱ�����ľ�ÿ��������������
��3���ڱ�֤�����������ܴ��ǰ���£����̳�����ÿ��2000Ԫ������Ӧ�ý����ۼ۶�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD���ܳ�Ϊ22 cm��AC��BD�ཻ�ڵ�O����AOD���ܳ�����AOB���ܳ�С3 cm����AB��________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ƻ�����A��B���ֲ�Ʒ��10�����������ɱ����������±���

(1)�������ƻ�����14��Ԫ����A��B���ֲ�ƷӦ�ֱ��������ټ���
(2)������Ͷ���ʽ���44��Ԫ���һ�������14��Ԫ���ʹ������ļ�������������
(3)��(2)�����£����ַ�������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������BCDE�ĸ��߷ֱ�ƽ����x����y�ᣬ������������ɵ�A��2��0��ͬʱ�������ؾ���BCDE�ı��������˶�������װ���ʱ�뷽����1����λ/�������˶��������Ұ�˳ʱ�뷽����2����λ/�������˶��������������˶���ĵ�2018�������ص�������ǣ�������

A. ��1����1�� B. ��2��0�� C. ����1��1�� D. ����1����1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����Rt��ABC������ACB = 90�㣮�뾶Ϊ1�ġ�A���AB�ཻ�ڵ�D�����AC�ཻ�ڵ�E������DE���ӳ������BC���ӳ��߽��ڵ�P��
��1������B = 30��ʱ����֤����ABC�ס�EPC��
��2������B = 30��ʱ������AP������AEP����BDP��������CE�ij���
��3����CE = 2��BD = BC������BPD������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���֪��A��0��a����B��0��b����y���ϣ��� C��m��b���ǵ���������һ�㣬������![]() ����ABC�������56��AC��x���ڵ�D��E��y�Ḻ�����ϵ�һ������.
����ABC�������56��AC��x���ڵ�D��E��y�Ḻ�����ϵ�һ������.
(1)��C�����ꣻ
(2)��ͼ2������DE����DE![]() AC��D�㣬EFΪ��AED��ƽ���ߣ���x����H�㣬�ҡ�DFE��90������֤��FDƽ�֡�ADO��
AC��D�㣬EFΪ��AED��ƽ���ߣ���x����H�㣬�ҡ�DFE��90������֤��FDƽ�֡�ADO��
(3)��ͼ3��E��y�Ḻ�������˶�ʱ����EC����PΪAC�ӳ�����һ�㣬EMƽ�� ��AEC����PM��EM��M�㣬PN��x����N�㣬PQƽ�֡�APN����x����Q�㣬��E���˶������У�![]() �Ĵ�С�Ƿ����仯�������䣬�����ֵ�����仯����˵������.
�Ĵ�С�Ƿ����仯�������䣬�����ֵ�����仯����˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڹ���ij��������Ʊʱ���蹺����Ʊ��Ϊx���ţ�������Ϊy��Ԫ�����������ֹ�����
����һ������λ��������10000Ԫ����õ�λ������Ʊ�ļ۸�Ϊÿ��60Ԫ�����ܷ��ã���������ѣ���Ʊ�ѣ�
��������������Ʊ��ʽ��ͼ��ʾ��
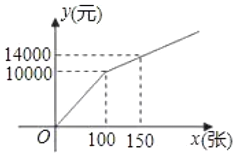
����������⣺
��1������һ�У�y��x�ĺ�����ϵʽΪ ��
����������0![]() x
x![]() 100ʱ��y��x�ĺ�����ϵʽΪ ��
100ʱ��y��x�ĺ�����ϵʽΪ ��
��x��100ʱ��y��x�ĺ�����ϵʽΪ ��
��2�����������������Ʊ����100�ţ��㽫ѡ����һ�ַ�����ʹ�ܷ�����ʡ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AC��EC�ֱ�Ϊ������ABCD��������EFCG�ĶԽ��ߣ���E����ABC�ڣ�����BF����CAE+��CBE=90����

��1����֤����CAE�ס�CBF��
��2����BE=1��AE=2����CE�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com