
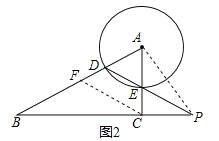
【题目】如图1,在Rt△ABC中,∠ACB = 90°.半径为1的⊙A与边AB相交于点D,与边AC相交于点E,连接DE并延长,与边BC的延长线交于点P.
(1)当∠B = 30°时,求证:△ABC∽△EPC;
(2)当∠B = 30°时,连接AP,若△AEP与△BDP相似,求CE的长;
(3)若CE = 2,BD = BC,求∠BPD的正切值.

【答案】(1)答案见解析;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)由已知条件易求∠A=60°,又因为AD=AE,所以△ADE是等边三角形,进而可得∠CEP=60°,由三角形内角和定理可求∠P=30°,继而可证明△ABC∽△EPC;
(2)根据∠B=30°,∠ACB=90°可得∠BAC=60°,从而得到△ADE是等边三角形,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BPD=30°,然后根据等角对等边的性质可得BD=PD,再根据△AEP与△BDP相似可得PE=AE,然后根据30°角所对的直角边等于斜边的一半即可求解;
(3)设BD=BC=x,表示出AB、AC的长度,然后利用勾股定理列式求出x的值为4,过点C作CF∥DP交AB于点F,再根据平行线分线段成比例定理求出DF=2,然后求出BF的长度,再次利用平行线分线段成比例定理求出CP的长度,然后根据正切的定义解答即可.
试题解析:解:(1)∵∠ACB=90°,∠B=30°,∴∠A=60°,∵AD=AE,∴△ADE是等边三角形,∴∠ADE=∠AED=60°,∴∠PEC=∠AED=60°,∵∠ACB=∠ECP=90°,∴∠P=30°,∴△ABC∽△EPC;
(2)∵∠B=30°,∠ACB=90°,∴∠BAC=90°﹣30°=60°,∴△ADE是等边三角形,在△BDP中,∠ADE=∠B+∠BPD,即60°=30°+∠BPD,解得∠BPD=30°,∴∠B=∠BPD,∴BD=PD,∵△AEP与△BDP相似,∴AE=PE,∵⊙A的半径为1,∴PE=1,在Rt△PCE中,CE=![]() PE=
PE=![]() ;
;
(3)设BD=BC=x,∵⊙A的半径为1,CE=2,∴AB=x+1,AC=2+1=3,∵∠ACB=90°,∴AC2+BC2=AB2,即32+x2=(x+1)2,解得x=4,过点C作CF∥DP交AB于点F,(如图2)
则![]() ,
,![]() ,即
,即![]() =
=![]() ,解得DF=2,∴BF=BD﹣DF=4﹣2=2,又由CF∥DP可得
,解得DF=2,∴BF=BD﹣DF=4﹣2=2,又由CF∥DP可得![]() ,即
,即![]() ,解得CP=4,∴tan∠BPD=
,解得CP=4,∴tan∠BPD=![]() =
=![]() =
=![]() .
.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】某学校计划在“阳光体育”活动课程中开设乒乓球、羽毛球、篮球、足球四个体育活动项目供学生选择.为了估计全校学生对这四个活动项目的选择情况,体育老师从全体学生中随机抽取了部分学生进行调查(规定每人必须并且只能选择其中的一个项目),并把调查结果绘制成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:
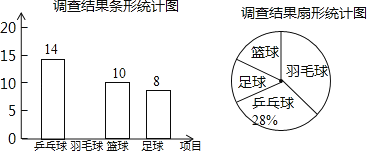
(1)参加这次调查的学生有 人,并根据已知数据补全条形统计图;
(2)求扇形统计图中“篮球”项目所对应扇形的圆心角度数;
(3)若该校共有800名学生,试估计该校选择“足球”项目的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高速公路的同一侧有A、B两城镇,如图,它们到高速公路所在直线MN的距离分别为AA′=2 km,BB′=4 km,A′B′=8 km.要在高速公路上A′、B′之间建一个出口P,使A、B两城镇到P的距离之和最小.求这个最短距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
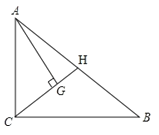
【题目】如图,在△ABC中,∠ACB=90°,点G是△ABC的重心,且AG⊥CG,CG的延长线交AB于H.
(1)求证:△CAG∽△ABC;
(2)求S△AGH:S△ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区教育部门准备在七年级开设兴趣课堂,以丰富学生课余生活.为了了解学生对音乐、书法、球类、绘画这四个兴趣小组的喜爱情况,在全区进行随机抽样调查,并根据收集的数据绘制了下面两幅统计图(信息不完整),请根据图中提供的信息,解答下面的问题:
(1) 此次共调查了 名同学;
(2) 将条形图补充完整,计算扇形统计图中音乐部分的圆心角的度数是 ;
(3) 如果该区七年级共有2 000名学生参加这4个课外兴趣小组,而每名教师最多只能辅导本组的20名学生,则绘画兴趣小组至少需要准备多少名教师?

查看答案和解析>>
科目:初中数学 来源: 题型:
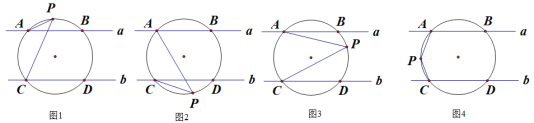
【题目】直线![]() ∥
∥![]() ,一圆交直线a,b分别于A、B、C、D四点,点P是圆上的一个动点,连接PA、PC.
,一圆交直线a,b分别于A、B、C、D四点,点P是圆上的一个动点,连接PA、PC.
(1)如图1,直接写出∠PAB、∠PCD、∠P之间的数量关系为 ;
(2)如图2,直接写出∠PAB、∠PCD、∠P之间的数量关系为
(3)如图3,求证:∠P=∠PAB+∠PCD;
(4)如图4,直接写出∠PAB、∠PCD、∠P之间的数量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在□ABCD中,E,F分别在BC,AD上,若想使四边形AFCE为平行四边形,须添加一个条件,这个条件可以是( )

①AF=CF;②AE=CF;③∠BAE=∠FCD;④∠BEA=∠FCE。
A. ①或② B. ②或③ C. ③或④ D. ①或③或④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣![]() x+1与y轴交于点D.
x+1与y轴交于点D.

(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC的三边长分别为6 cm、7.5 cm、9 cm,三角形DEF的一边长为4 cm.当三角形DEF的另两边长是下列哪一组时,这两个三角形相似( )
A. 2 cm、3 cm B. 4 cm、5 cm C. 5 cm、6 cm D. 6 cm、7 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com