
【题目】直线![]() ∥
∥![]() ,一圆交直线a,b分别于A、B、C、D四点,点P是圆上的一个动点,连接PA、PC.
,一圆交直线a,b分别于A、B、C、D四点,点P是圆上的一个动点,连接PA、PC.
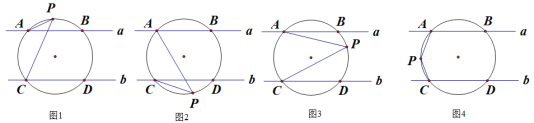
(1)如图1,直接写出∠PAB、∠PCD、∠P之间的数量关系为 ;
(2)如图2,直接写出∠PAB、∠PCD、∠P之间的数量关系为
(3)如图3,求证:∠P=∠PAB+∠PCD;
(4)如图4,直接写出∠PAB、∠PCD、∠P之间的数量关系为 .
【答案】(1)∠PCD=∠P+∠PAB;(2)∠PAB=∠P+∠PCD;(3)见解析;(4)∠PAB+∠P+∠PCD=360°.
【解析】
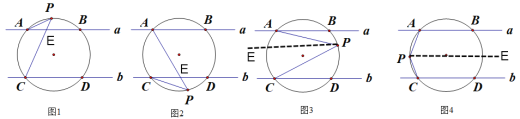
(1)方法一:设AB、PC相交于点E,由外角性质得:∠PEB=∠P+∠PAB,又因为a∥b,所以∠PEB=∠PCD,从而求解;方法二:过点P作PE∥AB;
(2)方法一:设AP、CD相交于点E,理由同(1)得∠PED=∠P+∠PCD,又因为a∥b,所以∠PED=∠PAB,从而求解;方法二:过点P作PE∥AB;
(3) 过点P作PE∥a,因为a∥b,所以PE∥b,所以∠PAB=∠APE,∠∠PCD =∠EPC,
又因为∠APC=∠APE+∠CPE,所以∠APC=∠PAB+∠PCD;
(4) ∠PAB+∠P+∠PCD=360°. 过点P作PE∥a,因为a∥b,所以PE∥b,所以∠PAB+∠APE=180°,∠PCD+∠CPE=180°,即∠PAB+∠APE+∠PCD+∠CPE=360°,从而求解;
解 :(1)∠PCD=∠P+∠PAB;
理由:设AB、PC相交于点E,由外角性质得:∠PEB=∠P+∠PAB,
∵a∥b,∴∠PEB=∠PCD,
∴∠PCD=∠P+∠PAB;
(2)∠PAB=∠P+∠PCD;
理由:设AP、CD相交于点E,理由同(1)得∠PED=∠P+∠PCD,
又∵a∥b,∴∠PED=∠PAB,
∴ ∠PAB=∠P+∠PCD ;
(3)过点P作PE∥a,∵a∥b,∴PE∥b,
∴∠PAB=∠APE,∠∠PCD =∠EPC,
∵∠APC=∠APE+∠CPE
∴∠APC=∠PAB+∠PCD;;
(4) ∠PAB+∠P+∠PCD=360°
理由:过点P作PE∥a,∵a∥b,∴PE∥b,
∴∠PAB+∠APE=180°,∠PCD+∠CPE=180°
∴∠PAB+∠APE+∠PCD+∠CPE=360°
即∠PAB+∠APC+∠PCD=360°.


 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】2018年俄罗斯世界杯组委会对世界杯比赛用球进行抽查,随机抽取了100个足球,检测每个足球的质量是否符合标准,超过或不足部分分别用正、负数来表示,记录如表:
与标准质量的差值(单位:克) | ﹣4 | ﹣2 | 0 | 1 | 3 | 6 |
个数 | 10 | 13 | 30 | 25 | 15 | 7 |
(1)平均每个足球的质量比标准质量多还是少?用你学过的方法合理解释;
(2)若每个足球标准质量为420克,则抽样检测的足球的总质量是多少克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线L1:y=bx+c与抛物线L2:y=ax2的两个交点坐标分别为A(m,4),B(1,1).
(1)求m的值;
(2)过动点P(n,0)且垂直于x轴的直线与L1,L2的交点分别为C,D,当点C位于点D上方时,请直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
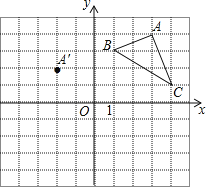
【题目】在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A′的坐标是(﹣2,2),现将△ABC平移.使点A变换为点A′,点B′、C′分别是B、C的对应点.
(1)请画出平移后的△A′B′C′(不写画法),并直接写出点B′的坐标:B′(_____________);
(2)若△ABC内部一点P的坐标为(a,b),则点P的对应点P′的坐标是(________________);
(3)求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB = 90°.半径为1的⊙A与边AB相交于点D,与边AC相交于点E,连接DE并延长,与边BC的延长线交于点P.
(1)当∠B = 30°时,求证:△ABC∽△EPC;
(2)当∠B = 30°时,连接AP,若△AEP与△BDP相似,求CE的长;
(3)若CE = 2,BD = BC,求∠BPD的正切值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=![]() ,AE=3,求AF的长.
,AE=3,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,等腰直角三角形AOB的斜边OB在x轴上,直线y=2x-2经过等腰直角三角形AOB的直角顶点A,交y轴于点C.
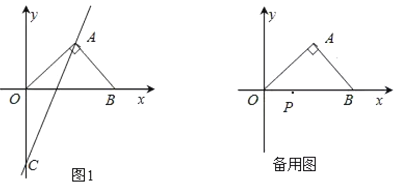
(1)点C坐标是( , );点A坐标是( , );
(2)若D是坐标平面内任意一点,使点A、C、O、D刚好能构成平行四边形,请直接写出符合条件的点D的坐标;
(3)若点P是x轴上一动点.点Q的坐标是(a,![]() ),△PAQ是以点A为直角顶点的等腰三角形.求出a的值并写出点Q的坐标.
),△PAQ是以点A为直角顶点的等腰三角形.求出a的值并写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,AB=10,BC=13,点P为边AD上一动点,点A’与点A关于BP对称,连结A’C,当△A’BC为等腰三角形时,AP的长度为()

A.2B.![]() C.2或
C.2或![]() D.2或
D.2或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】党的十六大提出全面建设小康社会,加快推进社会主义现代化,力争国民生产总值到2020年比2000年翻两番(“翻一番”表示为原来的2倍)在本世纪的头二十年(2001年~2020年),要实现这一目标,以十年为单位计算,设每个十年的国民生产总值的增长率都是![]() ,那么满足的方程为( )
,那么满足的方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com