
【题目】已知矩形ABCD,AB=10,BC=13,点P为边AD上一动点,点A’与点A关于BP对称,连结A’C,当△A’BC为等腰三角形时,AP的长度为()

A.2B.![]() C.2或
C.2或![]() D.2或
D.2或![]()
【答案】C
【解析】
①如图1,当A′B=A′C时,过A′作A′M⊥BC于M反向延长A′M交AD于N,则MN⊥AD,得到MN垂直平分BC和AD,根据轴对称的性质得到AB=A′B=10,∠PA′B=∠A=90°,根据勾股定理得到A′M=![]() ,根据相似三角形的性质即可得到结论;②当A′B=BC时,这种情况不存在;③如图2,当A′C=BC=13时,过A′作A′M⊥BC于M反向延长A′M交AD于N,则MN⊥AD,过C作CH⊥A′B于H,由勾股定理得到CH=
,根据相似三角形的性质即可得到结论;②当A′B=BC时,这种情况不存在;③如图2,当A′C=BC=13时,过A′作A′M⊥BC于M反向延长A′M交AD于N,则MN⊥AD,过C作CH⊥A′B于H,由勾股定理得到CH=![]() ,根据三角形的面积公式得到A′M=
,根据三角形的面积公式得到A′M=![]() ,根据相似三角形的性质即可得到结论.
,根据相似三角形的性质即可得到结论.
解:∵△A′BC为等腰三角形,
∴①如图1,当A′B=A′C时,过A′作A′M⊥BC于M反向延长A′M交AD于N,
则MN⊥AD,
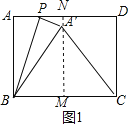
∴MN垂直平分BC和AD,
∵BC=13,
∴BM=AN=![]() ,
,
∵点A′与点A关于BP对称,
∴△ABP≌△A′BP,
∴AB=A′B=10,∠PA′B=∠A=90°,
∴A′M=![]() ,
,
∴A′N=MN-A′M=![]() ,
,
∵∠PA′N+∠A′PN=∠PA′N+∠BA′M=90°,
∴∠A′PN=∠BA′M,
∵∠PNA′=∠A′MB=90°,
∴△A′PN∽△BA′M,
∴![]() ,
,
∴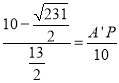 ,
,
∴A′P=![]() ,
,
∴AP=A′P=![]() ,
,
②当A′B=BC时,
∵A′B=AB=10,
∴这种情况不存在;
③如图2,当A′C=BC=13时,
过A′作A′M⊥BC于M反向延长A′M交AD于N,则MN⊥AD,过C作CH⊥A′B于H,
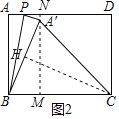
∴BH=![]() ×10=5,
×10=5,
∴CH=![]() ,
,
∴A′M=![]() ,
,
∴A′N=![]() ,BM=
,BM=![]() ,
,
由①知,![]() ,
,
∴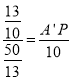 ,
,
∴A′P=AP=2,
综上所述,AP的长度为2或![]() ;
;
故选:C.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】为了丰富学生课余生活,某区教育部门准备在七年级开设兴趣课堂.为了了解学生对音乐、书法、球类、绘画这四个兴趣小组的喜爱情况,在全区进行随机抽样调查,并根据收集的数据绘制了下面两幅统计图(信息不完整),请根据图中提供的信息,解答下面的问题:
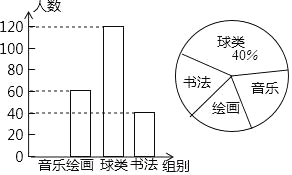
(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中音乐部分的圆心角的度数
(3)如果该区七年级共有2000名学生参加这4个课外兴趣小组,而每名教师最多只能辅导本组的20名学生,则绘画兴趣小组至少需要准备多少名教师?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() ∥
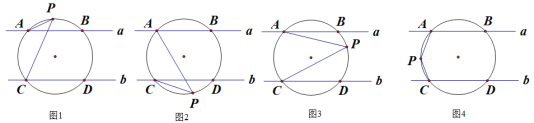
∥![]() ,一圆交直线a,b分别于A、B、C、D四点,点P是圆上的一个动点,连接PA、PC.
,一圆交直线a,b分别于A、B、C、D四点,点P是圆上的一个动点,连接PA、PC.
(1)如图1,直接写出∠PAB、∠PCD、∠P之间的数量关系为 ;
(2)如图2,直接写出∠PAB、∠PCD、∠P之间的数量关系为
(3)如图3,求证:∠P=∠PAB+∠PCD;
(4)如图4,直接写出∠PAB、∠PCD、∠P之间的数量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点E为AB中点,连接CE,将顶点B沿CE折叠至点P处,连接AP并延长交边CD于点F,
(1)判断四边形AECF为的形状并说明理由;
(2)若点P同时可看作是B点绕C点顺时针旋转60°得到,求证:△APB≌△ECP;
(3)若AB=6,BC=4,求![]() 的值
的值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣![]() x+1与y轴交于点D.
x+1与y轴交于点D.

(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接边境贸易博览会,组织部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A、B两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.
(1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.
(2)若搭配一个A种造型的成本是800元,搭配一个B种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的对角线交于点E,将△DCB沿CD翻折得到△DCF.
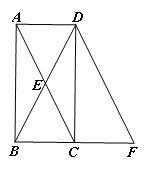
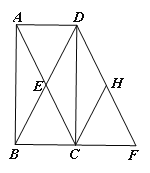
(1)求证:四边形ACFD是平行四边形;
(2)点H为DF的中点,连结CH,若AB=4,BC=2,求四边形ECHD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两个可以自由转动的均匀的转盘,甲转盘被分成3个面积相等
的扇形,乙转盘被分成4个面积相等的扇形,每一个扇形都标有相应的数字,同时转
动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为m,乙转盘中指针
所指区域内的数字为n(若指针指在边界线上时,重转一次,直到指针都指向一个区
域为止).

【1】请你用画树状图或列表格的方法求出|m+n|>1的概率
【2】直接写出点(m,n)落在函数y=- 图象上的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() 三点,其中a=
三点,其中a=![]() ,b,c满足关系式
,b,c满足关系式![]() ,P是第二象限内一点,连接PO,且P、A、C三点在一条直线上.
,P是第二象限内一点,连接PO,且P、A、C三点在一条直线上.
(1)求A、B、C三点的坐标;
(2)若规定:在三角形中,若两条边相等,则这两条边与第三边的夹角相等。如在△DEF中,DE=DF,则∠E=∠F.在本图中若PA=PO,AB=AC,CB⊥OB,垂足为B.求证:AB∥PO.
(3)如果在第二象限内有一点P(-2,![]() ),求四边形POBC的面积.
),求四边形POBC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com