
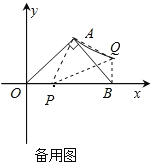
【题目】如图(1),在平面直角坐标系中,等腰直角三角形AOB的斜边OB在x轴上,直线y=2x-2经过等腰直角三角形AOB的直角顶点A,交y轴于点C.
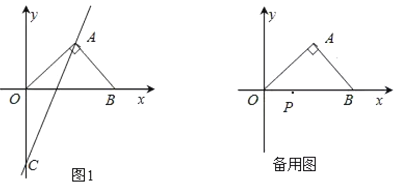
(1)点C坐标是( , );点A坐标是( , );
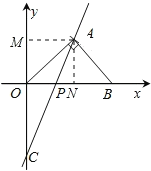
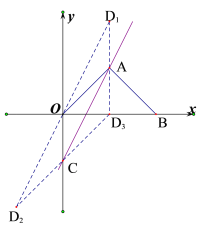
(2)若D是坐标平面内任意一点,使点A、C、O、D刚好能构成平行四边形,请直接写出符合条件的点D的坐标;
(3)若点P是x轴上一动点.点Q的坐标是(a,![]() ),△PAQ是以点A为直角顶点的等腰三角形.求出a的值并写出点Q的坐标.
),△PAQ是以点A为直角顶点的等腰三角形.求出a的值并写出点Q的坐标.
【答案】(1)0,-2,2,2;(2)![]() ,
,![]() ,
,![]() ;(3)a=4,Q(4,1).
;(3)a=4,Q(4,1).
【解析】
(1)过点A分别作AM⊥y轴于M点,AN⊥x轴于N点,根据等腰直角三角形的性质可设点A的坐标为(a,a),再把A点坐标代入y=2x-2,即可算出a的值,进而得到A点坐标,令x=0,代入y=2x-2,即可得到点C的坐标;
(2)画出草图,根据平行四边形的性质,分3种情况:当以OA为平行四边形的对角线时,当以OC为平行四边形的对角线时,当以AC为平行四边形的对角线时,分别求出点C的坐标,即可;
(3)连接AQ,AP,PQ,BQ,由SAS易证△APO≌△AQB,得出∠AOP=∠ABQ=45°,从而求得QB⊥OB,结合B点的坐标,即可得到点Q的坐标.
(1)过点A分别作AM⊥y轴于点M,AN⊥x轴于点N,
∵△AOB是等腰直角三角形,
∴ON=AN=BN,
∵∠MON=∠ANO=∠AMO=90°,
∴四边形ANOM是正方形,
∴AM=AN,
设点A的坐标为(a,a),
∵点A在直线y=2x2上,
∴a=2a2,
解得:a=2,
∴A(2,2),
令x=0,代入y=2x2得:y=-2,
∴C(0,-2).
故答案是:0,-2,2,2;
(2)∵A(2,2),C(0,-2),D是坐标平面内任意一点,使点A、C、O、D刚好能构成平行四边形,
∴当以OA为平行四边形的对角线时,![]() ,当以OC为平行四边形的对角线时,
,当以OC为平行四边形的对角线时,![]() ,当以AC为平行四边形的对角线时,
,当以AC为平行四边形的对角线时,![]() ,
,
综上所述,点D的坐标是:![]() ,
,![]() ,
,![]() ;
;
(3)连接AQ,AP,PQ,BQ,
∵△PAQ是以点A为直角顶点的等腰三角形,
∴AP=AQ,
∵∠OAB=∠PAQ=90°,
∴∠OAB∠PAB=∠PAQ∠PAB,
∴∠OAP=∠BAQ,
在△APO与△AQB中,
∵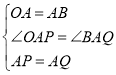 ,
,
∴△APO≌△AQB(SAS),
∴∠AOP=∠ABQ=45°,
∴∠OBQ=45°+45°=90°,
∴QB⊥OB,
∵A(2,2),
由第(1)题,可得OB=2AN=4,
∴B(4,0),
∵Q点的坐标是(a,![]() ),
),
∴a=4,
∴Q(4


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方
向依次不断移动,每次移动1个单位,其行走路线如下图所示.

(1)填写下列各点的坐标:A4( , )、A8( , )、A12( , );
(2)写出点A4n的坐标(n是正整数);
(3)指出蚂蚁从点A100到点A101的移动方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
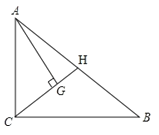
【题目】如图,在△ABC中,∠ACB=90°,点G是△ABC的重心,且AG⊥CG,CG的延长线交AB于H.
(1)求证:△CAG∽△ABC;
(2)求S△AGH:S△ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
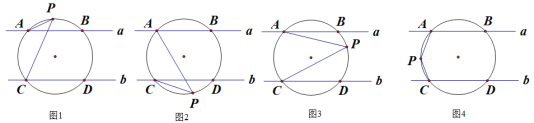
【题目】直线![]() ∥
∥![]() ,一圆交直线a,b分别于A、B、C、D四点,点P是圆上的一个动点,连接PA、PC.
,一圆交直线a,b分别于A、B、C、D四点,点P是圆上的一个动点,连接PA、PC.
(1)如图1,直接写出∠PAB、∠PCD、∠P之间的数量关系为 ;
(2)如图2,直接写出∠PAB、∠PCD、∠P之间的数量关系为
(3)如图3,求证:∠P=∠PAB+∠PCD;
(4)如图4,直接写出∠PAB、∠PCD、∠P之间的数量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在□ABCD中,E,F分别在BC,AD上,若想使四边形AFCE为平行四边形,须添加一个条件,这个条件可以是( )

①AF=CF;②AE=CF;③∠BAE=∠FCD;④∠BEA=∠FCE。
A. ①或② B. ②或③ C. ③或④ D. ①或③或④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点E为AB中点,连接CE,将顶点B沿CE折叠至点P处,连接AP并延长交边CD于点F,
(1)判断四边形AECF为的形状并说明理由;
(2)若点P同时可看作是B点绕C点顺时针旋转60°得到,求证:△APB≌△ECP;
(3)若AB=6,BC=4,求![]() 的值
的值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣![]() x+1与y轴交于点D.
x+1与y轴交于点D.

(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的对角线交于点E,将△DCB沿CD翻折得到△DCF.
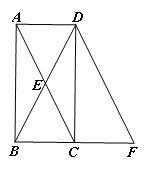
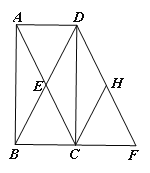
(1)求证:四边形ACFD是平行四边形;
(2)点H为DF的中点,连结CH,若AB=4,BC=2,求四边形ECHD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
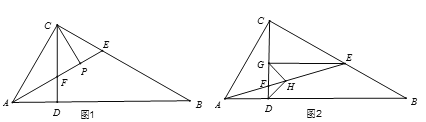
【题目】已知:在Rt△ABC中,∠ACB=90°,过点C作CD⊥AB于点D,点E是BC上一点,连接AE交CD于点F.
(1)如图1,若AE平分∠CAB,CP平分∠BCD,求证:FP=EP;
(2)如图2,若CE=CA,过点E作EG⊥CD于点G,点H为AE的中点,连接DH,GH,判断△GDH的形状,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com