
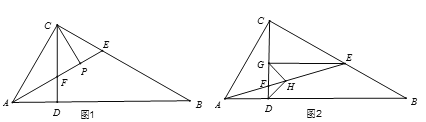
【题目】已知:在Rt△ABC中,∠ACB=90°,过点C作CD⊥AB于点D,点E是BC上一点,连接AE交CD于点F.
(1)如图1,若AE平分∠CAB,CP平分∠BCD,求证:FP=EP;
(2)如图2,若CE=CA,过点E作EG⊥CD于点G,点H为AE的中点,连接DH,GH,判断△GDH的形状,并证明.
【答案】(1)证明见解析;(2)△GDH是等腰直角三角形,理由见解析.
【解析】
(1)由CD⊥AB,∠ACB=90°可得∠ACD=∠B,继而根据角平分线的定义以及三角形外角的性质可得∠CFE=∠CEF,得到CF=CE,再根据等腰三角形的性质即可得证;
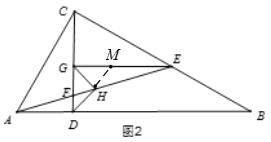
(2)如图2,延长DH交EG于点M,证明△ACD≌△CEG,从而可得AD=CG,CD=GE,再证明△ADH≌△EMH,从而可得EM=AD,DH=MH,继而根据CD=CG+DG,EG=EM+MG,可得DG=MG,判断出△DGM是等腰直角三角形,再根据DH=MH,可得HG⊥DH,GH=DH,从而可得△GDH是等腰直角三角形.
(1)∵CD⊥AB,∠ACB=90°,
∴∠ACD+∠CAD=90°,∠B+∠CAB=90°,
∴∠ACD=∠B,
∵AE平分∠CAB,
∴∠CAE=∠BAE,
∵∠CFE=∠ACD+∠CAE,∠CEF=∠B+∠BAE,
∴∠CFE=∠CEF,
∴CF=CE,
又∵CP平分∠BCD,
∴FP=EP;
(2)△GDH是等腰直角三角形,理由如下:
如图2,延长DH交EG于点M,
∵EG⊥CD,
∴∠CGE=∠EGD=90°,
∴∠CEG+∠ECG=90°,
∵∠ACD+∠ECG=∠ACB=90°,
∴∠ACD=∠CEG,
又∵∠ADC=90°=∠CGE,AC=CE,
∴△ACD≌△CEG,
∴AD=CG,CD=GE,
∵∠ACD=∠B,
∴∠CEG=∠B,
∴EG//AD,
∴∠HAD=∠HEG,∠ADH=∠EMH,
又∵AH=EH,
∴△ADH≌△EMH,
∴EM=AD,DH=MH,
∵CD=CG+DG,EG=EM+MG,
∴DG=MG,
∴△DGM是等腰直角三角形,
又∵DH=MH,
∴HG⊥DH,GH=DH,
∴△GDH是等腰直角三角形.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,等腰直角三角形AOB的斜边OB在x轴上,直线y=2x-2经过等腰直角三角形AOB的直角顶点A,交y轴于点C.
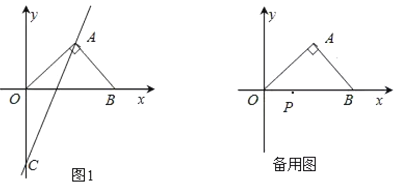
(1)点C坐标是( , );点A坐标是( , );
(2)若D是坐标平面内任意一点,使点A、C、O、D刚好能构成平行四边形,请直接写出符合条件的点D的坐标;
(3)若点P是x轴上一动点.点Q的坐标是(a,![]() ),△PAQ是以点A为直角顶点的等腰三角形.求出a的值并写出点Q的坐标.
),△PAQ是以点A为直角顶点的等腰三角形.求出a的值并写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3%的损耗,第二次购进的水果有5%的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】党的十六大提出全面建设小康社会,加快推进社会主义现代化,力争国民生产总值到2020年比2000年翻两番(“翻一番”表示为原来的2倍)在本世纪的头二十年(2001年~2020年),要实现这一目标,以十年为单位计算,设每个十年的国民生产总值的增长率都是![]() ,那么满足的方程为( )
,那么满足的方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在![]() 处测得灯塔
处测得灯塔![]() 在北偏东
在北偏东![]() 方向上,继续航行1小时到达
方向上,继续航行1小时到达![]() 处,此时测得灯塔
处,此时测得灯塔![]() 在北偏东
在北偏东![]() 方向上.
方向上.
(1)求![]() 的度数;
的度数;
(2)已知在灯塔![]() 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图17-Z-11,小红同学要测量A,C两地的距离,但A,C之间有一水池,不能直接测量,于是她在A,C同一水平面上选取了一点B,点B可直接到达A,C两地.她测量得到AB=80米,BC=20米,∠ABC=120°.请你帮助小红同学求出A,C两地之间的距离.(结果精确到1米,参考数据: ![]() ≈4.6)
≈4.6)
![]()
图17-Z-11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对七年级学生数学学期成绩的评价规定如下:学期评价得分由期中测试成绩(满分150分)和期末测试成绩(满分150分)两部分组成,其中期中测试成绩占30%,期末测试成绩占70%,当学期评价得分大于或等于130分时,该生数学学期成绩评价为优秀.(注:期中、期末成绩分数取整数)
(1)小明的期中成绩和期末测试成绩两项得分之和为260分,学期评价得分为132分,则小明期中测试成绩和期末测试成绩各得多少分?
(2)某同学期末测试成绩为120分,他的综合评价得分有可能达到优秀吗?为什么?
(3)如果一个同学学期评价得分要达到优秀,他的期末测试成绩至少要多少分(结果保留整数)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程kx2-4x+2=0有实数根.
(1)求k的取值范围;
(2)若ABC中,AB=AC=2,AB、BC的长是方程kx2-4x+2=0的两根,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下表回答问题:
x | 16 | 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 |
x2 | 256 | 259.21 | 262.44 | 265.69 | 268.96 | 272.25 | 175.56 | 278.89 | 282.24 |
(1)272.25的平方根是
(2)![]() = ,
= , ![]() = ,
= , ![]() =
=
(3)设![]() 的整数部分为a,求﹣4a的立方根.
的整数部分为a,求﹣4a的立方根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com