
【题目】某中学对七年级学生数学学期成绩的评价规定如下:学期评价得分由期中测试成绩(满分150分)和期末测试成绩(满分150分)两部分组成,其中期中测试成绩占30%,期末测试成绩占70%,当学期评价得分大于或等于130分时,该生数学学期成绩评价为优秀.(注:期中、期末成绩分数取整数)
(1)小明的期中成绩和期末测试成绩两项得分之和为260分,学期评价得分为132分,则小明期中测试成绩和期末测试成绩各得多少分?
(2)某同学期末测试成绩为120分,他的综合评价得分有可能达到优秀吗?为什么?
(3)如果一个同学学期评价得分要达到优秀,他的期末测试成绩至少要多少分(结果保留整数)?
【答案】(1)小明同学期末测试成绩为135分,期中测试成绩为125分;(2)不存在;(3)121分.
【解析】
(1)设小明同学期末测试成绩为x分,期中测试成绩为y分,根据题意列出方程组,求出方程组的解即可得到结果;
(2)根据题意计算出他的综合评价成绩,判断即可;
(3)根据题意列出不等式,求出不等式的解集即可得到结果.
(1)设小明同学期末测试成绩为x分,期中测试成绩为y分,
由题意,得
![]() ,
,
解得![]() ,
,
答:小明同学期末测试成绩为135分,期中测试成绩为125分;
(2)不可能.
由题意可得:130-120×70%=46,
46÷30%=153![]() >150,故不可能;
>150,故不可能;
(3)设平时成绩为满分,即150分,综合成绩为150×30%=45,
设期末测试成绩为m分,根据题意可得:45+70%m≥130,
解得:m≥121![]() ,
,
答:他的期末测试成绩应该至少为121分.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣![]() x+1与y轴交于点D.
x+1与y轴交于点D.

(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC的三边长分别为6 cm、7.5 cm、9 cm,三角形DEF的一边长为4 cm.当三角形DEF的另两边长是下列哪一组时,这两个三角形相似( )
A. 2 cm、3 cm B. 4 cm、5 cm C. 5 cm、6 cm D. 6 cm、7 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
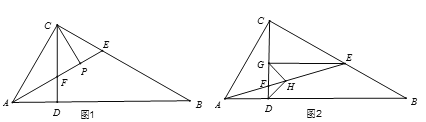
【题目】已知:在Rt△ABC中,∠ACB=90°,过点C作CD⊥AB于点D,点E是BC上一点,连接AE交CD于点F.
(1)如图1,若AE平分∠CAB,CP平分∠BCD,求证:FP=EP;
(2)如图2,若CE=CA,过点E作EG⊥CD于点G,点H为AE的中点,连接DH,GH,判断△GDH的形状,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
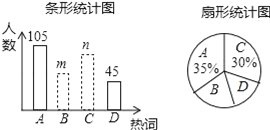
【题目】2017年3月全国两会胜利召开,某学校就两会期间出现频率最高的热词:A.蓝天保卫战,B.不动产保护,C.经济增速,D.简政放权等进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)从该校学生中随机抽取一个最关注热词D的学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() 三点,其中a=
三点,其中a=![]() ,b,c满足关系式
,b,c满足关系式![]() ,P是第二象限内一点,连接PO,且P、A、C三点在一条直线上.
,P是第二象限内一点,连接PO,且P、A、C三点在一条直线上.
(1)求A、B、C三点的坐标;
(2)若规定:在三角形中,若两条边相等,则这两条边与第三边的夹角相等。如在△DEF中,DE=DF,则∠E=∠F.在本图中若PA=PO,AB=AC,CB⊥OB,垂足为B.求证:AB∥PO.
(3)如果在第二象限内有一点P(-2,![]() ),求四边形POBC的面积.
),求四边形POBC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )

A. 1<m<11 B. 2<m<22 C. 10<m<12 D. 5<m<6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(2,1),B(﹣1,1),C(﹣1,﹣3),D(2,﹣3),点P从点A出发,以每秒1个单位长度的速度沿A﹣B﹣C﹣D﹣A…的规律在图边形ABCD的边上循环运动,则第2019秒时点P的坐标为( )

A. (1,1)B. (0,1)C. (﹣1,1)D. (2,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的周长为20,对角线AC长为![]() ,点E、F分别为AC、BC边上的动点.
,点E、F分别为AC、BC边上的动点.

(1)直接写出菱形ABCD的面积:_______;
(2)直接写出BE+EF的最小值_______;并在图中作出此时的点E和点F.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com