
����Ŀ��ij�̳�Ҫ��Ӫһ�������е��ľߣ�����Ϊ20Ԫ�M���������η��֣������ۼ�Ϊ25Ԫ�M��ʱ��ÿ�����������250�������ۼ�ÿ����1Ԫ��ÿ����������ͼ���10����
��1��д���̳����������ľߣ�ÿ�����õ���������![]() ��Ԫ�������۵���
��Ԫ�������۵���![]() ��Ԫ��֮��ĺ�����ϵʽ��
��Ԫ��֮��ĺ�����ϵʽ��
��2�������۵���Ϊ����Ԫʱ�����ľ�ÿ��������������
��3���ڱ�֤�����������ܴ��ǰ���£����̳�����ÿ��2000Ԫ������Ӧ�ý����ۼ۶�Ϊ����Ԫ��
���𰸡���1��![]() ��
��
��2����![]() ʱ��
ʱ�� ![]() ȡ�����ֵ2250��
ȡ�����ֵ2250��
��3���ڱ�֤�����������ܴ��ǰ���£����̳�����ÿ��2000Ԫ������Ӧ�ý����ۼ۶�Ϊ30Ԫ.
�������������������1����������=250��10��x��25����������������ÿ������=�������г�������ϵʽ���ɣ�
��2��ֱ�����ö��κ�����ֵ�ó�����
��3��������1��ʽ�г����̣��������������
����������⣺��1��![]() ��
��
��2����![]()
����![]() ������
������![]() ʱ��
ʱ�� ![]() ȡ�����ֵ2250��
ȡ�����ֵ2250��
��3���ڣ�1���У���w=2000ʱ���� ![]() ����
����![]() �����
�����![]() ��
�� ![]() ��
��
��![]() ʱ������Ϊ200������
ʱ������Ϊ200������![]() ʱ������Ϊ100��С��200�����������⣬Ӧ��ȥ������
ʱ������Ϊ100��С��200�����������⣬Ӧ��ȥ������![]() ��
��
���ڱ�֤�����������ܴ��ǰ���£����̳�����ÿ��2000Ԫ������Ӧ�ý����ۼ۶�Ϊ30Ԫ��


 �����Ծ�ϵ�д�
�����Ծ�ϵ�д� �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У��뾶��Ϊ1����λ���ȵİ�ԲO1��O2����O3�������һ��ƽ�������ߣ���P��ԭ��O���������������������˶����ٶ�Ϊÿ��![]() ����λ���ȣ����2018��ʱ����P�������ǣ�������
����λ���ȣ����2018��ʱ����P�������ǣ�������

A. ��2017��0��B. ��2018����1��C. ��2017��1��D. ��2018��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y��ax2��bx��c��a��0���Ķ���ΪC��1��4������x����A��B���㣬��y���ڵ� D�����е�B������Ϊ��3��0��.
��1���������ߵĽ���ʽ��
��2����ͼ2������A��ֱ���������߽��ڵ�E����y���ڵ�F�����е�E�ĺ�����Ϊ2����ֱ��PQΪ�����ߵĶԳ��ᣬ��GΪֱ��PQ�ϵ�һ���㣬��x�����Ƿ����һ��H��ʹD��G��H��F�ĵ���Χ�ɵ��ı����ܳ���С�������ڣ���������Сֵ����G��H�����ꣻ�������ڣ���˵������.
��3����ͼ3�������������Ƿ����һ��T������T��x��Ĵ��ߣ�����Ϊ��M������M��MN��BD�����߶�AD�ڵ�N������MD��ʹ��DNM�ס�BMD�������ڣ������T�����ꣻ�������ڣ���˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ȫУ1800��ѧ����ѧУ���õ���١����ࡢ�ܲ�������ӵȿ����������Ŀ��ϲ���������ȫУ��Χ�������ȡ��������ѧ������������ϲ����������Ŀ��ÿ��ֻѡһ��������ʾ����飬�����ݽ�����ͳ�Ʋ����Ƴ�����ͼ��ʾ��Ƶ���ֲ�ֱ��ͼ������ͳ��ͼ��������������
��1����ȫƵ���ֲ�ֱ��ͼ��
��2��������ͳ��ͼ�б�ʾ�����������Ŀ����Բ�ĽǵĶ�����
��3�����Ƹ�У1800��ѧ�����ж�������ϲ��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͨ��������롢������չ�о�������Ŀ���ɴﵽ��һ��֪һ���Ŀ�ģ�������һ��������
ԭ������ͼ������![]() �ֱ���������
�ֱ���������![]() �ı�
�ı�![]() ����
���� ![]() ������
������![]() ����
����![]() ����˵�����ɣ�
����˵�����ɣ�

��1��˼·����
��Ϊ![]() ������
������![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת90����
��ʱ����ת90����![]() ����ʹ
����ʹ![]() ��
��![]() �غϣ���Ϊ
�غϣ���Ϊ![]() ������
������![]() ����
����![]() ���ߣ�
���ߣ�
���� ����֤![]() ����
����![]() .��֤����
.��֤����
��2���������
��ͼ�����ı���![]() ����
���� ![]() ��
�� ![]() ����
����![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ����
���� ![]() .��
.��![]() ������ֱ������
������ֱ������![]() ��
��![]() ���������ϵʱ��
���������ϵʱ�� ![]() ��Ȼ��������֤����
��Ȼ��������֤����
��3��������չ
��ͼ������![]() ����
���� ![]() ����
����![]() ���ڱ�
���ڱ�![]() ������
������![]() .����
.����![]() Ӧ����ĵ�����ϵ����д��֤�����̣�
Ӧ����ĵ�����ϵ����д��֤�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�ƻ��ڡ�������������γ��п���ƹ������ë�����������ĸ��������Ŀ��ѧ��ѡ��Ϊ�˹���ȫУѧ�������ĸ����Ŀ��ѡ�������������ʦ��ȫ��ѧ���������ȡ�˲���ѧ�����е��飨�涨ÿ�˱��벢��ֻ��ѡ�����е�һ����Ŀ�������ѵ��������Ƴ���ͼ��ʾ�IJ�����������ͳ��ͼ������ͳ��ͼ���������ͼ����Ϣ����������⣺
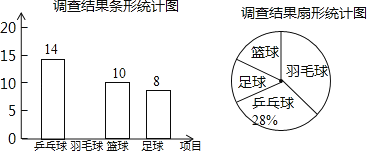
��1���μ���ε����ѧ���� �ˣ���������֪���ݲ�ȫ����ͳ��ͼ��
��2��������ͳ��ͼ�С�������Ŀ����Ӧ���ε�Բ�ĽǶ�����
��3������У����800��ѧ�����Թ��Ƹ�Уѡ��������Ŀ��ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�P�ǶԽ���BD�ϵ�һ�㣬��E��AD���ӳ����ϣ��ҡ�PAE=��E��PE��CD�ڵ�F��

��1����֤��PC=PE��
��2�����CPE�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ƻ�����12�Ų�����һ�����ӣ�������12�ѣ����ִӼס������̳��˽ͬһ�ͺŵIJ������۶�Ϊÿ��200Ԫ�����α��۶�Ϊÿ��50Ԫ�����̳��涨��ÿ����һ�Ų�������һ�Ѳ��Σ����̳��涨�����в��������ξ������۵İ��������ۣ���ô��ʲô����µ����̳�������Żݣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����������������꼶������Ȥ���ã��Էḻѧ���������Ϊ���˽�ѧ�������֡��鷨�����ࡢ�滭���ĸ���ȤС���ϲ���������ȫ����������������飬�������ռ������ݻ�������������ͳ��ͼ����Ϣ���������������ͼ���ṩ����Ϣ�������������⣺
(1) �˴ι������� ��ͬѧ��
(2) ������ͼ������������������ͳ��ͼ�����ֲ��ֵ�Բ�ĽǵĶ����� ��
(3) ����������꼶����2 000��ѧ���μ���4��������ȤС�飬��ÿ����ʦ���ֻ�ܸ��������20��ѧ������滭��ȤС��������Ҫ����������ʦ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com