
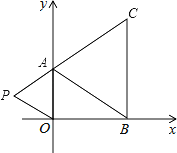
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпyЃНax2ЃЋbxЃЋcЃЈaЁй0ЃЉЕФЖЅЕуЮЊCЃЈ1ЃЌ4ЃЉЃЌНЛxжсгкAЁЂBСНЕуЃЌНЛyжсгкЕу DЃЌЦфжаЕуBЕФзјБъЮЊЃЈ3ЃЌ0ЃЉ.
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЙ§ЕуAЕФжБЯпгыХзЮяЯпНЛгкЕуEЃЌНЛyжсгкЕуFЃЌЦфжаЕуEЕФКсзјБъЮЊ2ЃЌШєжБЯпPQЮЊХзЮяЯпЕФЖдГЦжсЃЌЕуGЮЊжБЯпPQЩЯЕФвЛЖЏЕуЃЌдђxжсЩЯЪЧЗёДцдквЛЕуHЃЌЪЙDЁЂGЁЂHЁЂFЫФЕуЫљЮЇГЩЕФЫФБпаЮжмГЄзюаЁЃЛШєДцдкЃЌЧѓГіетИізюаЁжЕМАЕуGЁЂHЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЃЈ3ЃЉШчЭМ3ЃЌдкХзЮяЯпЩЯЪЧЗёДцдквЛЕуTЃЌЙ§ЕуTзїxжсЕФДЙЯпЃЌДЙзуЮЊЕуMЃЌЙ§ЕуMзїMNЁЮBDЃЌНЛЯпЖЮADгкЕуNЃЌСЌНгMDЃЌЪЙЁїDNMЁзЁїBMDЁЃШєДцдкЃЌЧѓГіЕуTЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.

ЁОД№АИЁПЃЈ1ЃЉyЃНЃ(xЃ1)2ЃЋ4ЃЛЃЈ2ЃЉЫФБпаЮDFHGЕФжмГЄзюаЁЮЊ![]() ЃЛЃЈ3ЃЉЕуTЕФзјБъЮЊЃЈ
ЃЛЃЈ3ЃЉЕуTЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉ
ЃЉ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЩшХзЮяЯпЕФНтЮіЪНЮЊЃК ![]() ШЛКѓНЋЕу
ШЛКѓНЋЕу![]() ЕФзјБъДњШыКЏЪ§НтЮіЪНМДПЩЧѓЕУДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЕФзјБъДњШыКЏЪ§НтЮіЪНМДПЩЧѓЕУДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉзї![]() Йигк
Йигк![]() жсЕФЖдГЦЕу
жсЕФЖдГЦЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() жсгк
жсгк![]() ЃЌНЛЖдГЦжс
ЃЌНЛЖдГЦжс![]() гк
гк![]() ЃЌЫФБпаЮ
ЃЌЫФБпаЮ![]() ЕФжмГЄМДЮЊзюаЁЃЌдђИљОнЬтвтМДПЩЧѓЕУетИізюаЁжЕМАЕу
ЕФжмГЄМДЮЊзюаЁЃЌдђИљОнЬтвтМДПЩЧѓЕУетИізюаЁжЕМАЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉЪзЯШЩш![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЧѓЕУ
ЧѓЕУ![]() гы
гы![]() ЕФГЄЃЌгЩЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэЃЌЧѓЕУ
ЕФГЄЃЌгЩЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэЃЌЧѓЕУ![]() ЕФГЄЃЌШЛКѓгЩЯрЫЦШ§НЧаЮЖдгІБпГЩБШР§ЃЌМДПЩЕУ
ЕФГЄЃЌШЛКѓгЩЯрЫЦШ§НЧаЮЖдгІБпГЩБШР§ЃЌМДПЩЕУ![]() дђПЩЕУЕНЙигк
дђПЩЕУЕНЙигк![]() ЕФвЛдЊЖўДЮЗНГЬЃЌНтЗНГЬМДПЩЧѓЕУД№АИЃЎ
ЕФвЛдЊЖўДЮЗНГЬЃЌНтЗНГЬМДПЩЧѓЕУД№АИЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЩшЫљЧѓХзЮяЯпЕФНтЮіЪНЮЊЃК ![]() вРЬтвтЃЌНЋЕу
вРЬтвтЃЌНЋЕу![]() ДњШыЃЌЕУЃК
ДњШыЃЌЕУЃК ![]()
НтЕУЃК ![]()
ЁрЫљЧѓХзЮяЯпЕФНтЮіЪНЮЊЃК ![]()
![]() Дцдк.ШчЭМЃЌ
Дцдк.ШчЭМЃЌ

ХзЮяЯпЕФЖдГЦжсЗНГЬЮЊЃКx=1ЃЌ
ЁпЕуEЕФКсзјБъЮЊ2ЃЌ
Ёрy=4+4+3=3ЃЌ
ЁрЕуE(2,3)ЃЌ
ЁрЩшжБЯпAEЕФНтЮіЪНЮЊЃКy=kx+bЃЌ
![]()
![]()
ЁржБЯпAEЕФНтЮіЪНЮЊЃКy=x+1ЃЌ
ЁрЕуF(0,1)ЃЌ
ЁпD(0,3)ЃЌ
ЁрDгыEЙигкx=1ЖдГЦ,
зїFЙигкxжсЕФЖдГЦЕуFЁф(0,1)ЃЌ
СЌНгEFЁфНЛxжсгкHЃЌНЛЖдГЦжсx=1гкGЃЌ
ЫФБпаЮDFHGЕФжмГЄМДЮЊзюаЁЃЌ
ЩшжБЯпEFЁфЕФНтЮіЪНЮЊЃКy=mx+nЃЌ
![]() НтЕУЃК
НтЕУЃК ![]()
ЁржБЯпEFЁфЕФНтЮіЪНЮЊЃКy=2x1ЃЌ
ЁрЕБy=0ЪБ,2x1=0,ЕУ![]()
МД![]()
ЕБx=1ЪБЃЌy=1ЃЌ
ЁрG(1,1)ЃЛ
ЁрDF=2, 
ЁрЪЙD.G,HЁЂFЫФЕуЫљЮЇГЩЕФЫФБпаЮжмГЄзюаЁжЕЮЊЃК
![]()
(3)Дцдк.

![]()
ЩшM(c,0)ЃЌ
![]()
![]()
МД![]()
![]()
вЊЪЙЁїDNMЁзЁїBMDЃЌ
аш![]() МД
МД![]()
ПЩЕУЃК ![]()
НтЕУЃК ![]() Лђc=3(ЩсШЅ).
Лђc=3(ЩсШЅ).
ЕБ![]() ЪБ,
ЪБ, ![]()
ЁрДцдк,ЕуTЕФзјБъЮЊ![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЯТУцжБНЧзјБъЯЕжаЃЌвбжЊAЃЈ0ЃЌaЃЉЃЌBЃЈbЃЌ0ЃЉЃЌCЃЈbЃЌcЃЉШ§ЕуЃЌЦфжаaЁЂbЁЂcТњзуЙиЯЕЪН![]() +ЃЈbЉ3ЃЉ2=0ЃЌЃЈcЉ4ЃЉ2Ём0
+ЃЈbЉ3ЃЉ2=0ЃЌЃЈcЉ4ЃЉ2Ём0
ЃЈ1ЃЉЧѓaЁЂbЁЂcЕФжЕЃЛ
ЃЈ2ЃЉШчЙћдкЕкЖўЯѓЯоФкгавЛЕуPЃЈЉmЃЌ![]() ЃЉЃЌЧыгУКЌmЕФЪНзгБэЪОЫФБпаЮABOPЕФУцЛ§ЃЛ
ЃЉЃЌЧыгУКЌmЕФЪНзгБэЪОЫФБпаЮABOPЕФУцЛ§ЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЪЧЗёДцдкЕуPЃЌЪЙЫФБпаЮABOPЕФУцЛ§гыЁїABCЕФУцЛ§ЯрЕШЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋЫФеХБпГЄИїВЛЯрЭЌЕФе§ЗНаЮжНЦЌАДШчЭМЗНЪНЗХШыОиаЮ![]() Фк(ЯрСкжНЦЌжЎМфЛЅВЛжиЕўвВЮоЗьЯЖ)ЃЌЮДБЛЫФеХе§ЗНаЮжНЦЌИВИЧЕФВПЗжгУвѕгАБэЪОЃЎЩшгвЩЯНЧгызѓЯТНЧвѕгАВПЗжЕФжмГЄЕФВюЮЊ
Фк(ЯрСкжНЦЌжЎМфЛЅВЛжиЕўвВЮоЗьЯЖ)ЃЌЮДБЛЫФеХе§ЗНаЮжНЦЌИВИЧЕФВПЗжгУвѕгАБэЪОЃЎЩшгвЩЯНЧгызѓЯТНЧвѕгАВПЗжЕФжмГЄЕФВюЮЊ![]() ЃЎШєжЊЕР
ЃЎШєжЊЕР![]() ЕФжЕЃЌдђВЛашВтСПОЭФмжЊЕРжмГЄЕФе§ЗНаЮЕФБъКХЮЊЃЈ ЃЉ
ЕФжЕЃЌдђВЛашВтСПОЭФмжЊЕРжмГЄЕФе§ЗНаЮЕФБъКХЮЊЃЈ ЃЉ

A.ЂйB.ЂкC.ЂлD.Ђм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
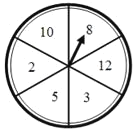
ЁОЬтФПЁПШчЭМЪЧаЁУїДгбЇаЃЕНМвааНјЕФТЗГЬs(Уз)гыЪБМфt(Зж)ЕФЭМЯѓЃЌЙлВьЭМЯѓЃЌДгжаЕУЕНШчЯТаХЯЂЃКЂйбЇаЃРыаЁУїМв1000УзЃЛЂкаЁУїгУСЫ20ЗжжгЕНМвЂлаЁУїЧА10ЗжжгзпСЫТЗГЬЕФвЛАыЃЛЂмаЁУїКѓ10ЗжжгБШЧА10ЗжжгзпЕУПьЃЌЦфжае§ШЗЕФга(ЁЁЁЁ)

A. ЂйЂкЂлB. ЂйЂкЂмC. ЂкЂлЂмD. ЂйЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁССЁЂаЁгБЕФЪжЩЯЖМгаСНИљГЄЖШЗжБ№ЮЊ5ЁЂ8ЕФФОАєЃЌаЁССгыаЁгБЖМЯыЭЈЙ§зЊЖЏзЊХЬгЮЯЗРДЛёШЁЕкШ§ИљФОАєЃЌШчЭМЃЌвЛИіОљдШЕФзЊХЬБЛЦНОљЗжГЩ6ЕШЗнЃЌЗжБ№БъгаФОАєЕФГЄЖШ2ЃЌ3ЃЌ5ЃЌ8ЃЌ10ЃЌ12ет6ИіЪ§зжЃЎаЁССгыаЁгБИїзЊЖЏзЊХЬвЛДЮЃЌЭЃжЙКѓЃЌжИеыжИЯђЕФЪ§зжМДЮЊзЊГіЕФЕкШ§ИљФОАєЕФГЄЖШЃЎШєШ§ИљФОАєФмзщГЩШ§НЧаЮдђаЁССЛёЪЄЃЌШ§ИљФОАєФмзщГЩЕШбќШ§НЧаЮдђаЁгБЛёЪЄЃЎ
(1)аЁССЛёЪЄЕФИХТЪЪЧЁЁ ЁЁЃЛ
(2)аЁгБЛёЪЄЕФИХТЪЪЧЁЁ ЁЁЃЛ
(3)ЧыФугУетИізЊХЬЩшМЦвЛИігЮЯЗЃЌЪЙЕУЖдаЁССгыаЁгБОљЪЧЙЋЦНЕФЃЛ
(4)аЁгБЗЂЯжЃЌЫ§СЌајзЊЖЏзЊХЬ10ДЮЃЌЖМУЛзЊЕН5КЭ8ЃЌФмВЛФмОЭЫЕаЁгБЛёЪЄЕФПЩФмадЮЊ0ЃПЮЊЪВУДЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAЁЂEЁЂFЁЂDЫФЕудкЭЌвЛжБЯпЩЯЃЌCEЁЮBFЃЌCE=BFЃЌЁЯB=ЁЯCЃЎЃЈ1ЃЉЁїABFгыЁїDCEШЋЕШТ№ЃПЧыЫЕУїРэгЩЃЛЃЈ2ЃЉABгыCDЦНааТ№ЃПЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=AC=2ЃЌЁЯB=ЁЯC=40ЁуЃЌЕуDдкЯпЖЮBCЩЯдЫЖЏЃЈDВЛгыBЁЂCжиКЯЃЉЃЌСЌНгADЃЌзїЁЯADE=40ЁуЃЌDEНЛЯпЖЮACгкEЃЎ
ЃЈ1ЃЉЕБЁЯBDA=115ЁуЪБЃЌЁЯEDC=______ЁуЃЌЁЯDEC=______ЁуЃЛЕуDДгBЯђCдЫЖЏЪБЃЌЁЯBDAж№НЅБф______ЃЈЬюЁАДѓЁБЛђЁАаЁЁБЃЉЃЛ
ЃЈ2ЃЉЕБDCЕШгкЖрЩйЪБЃЌЁїABDЁеЁїDCEЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкЕуDЕФдЫЖЏЙ§ГЬжаЃЌЁїADEЕФаЮзДПЩвдЪЧЕШбќШ§НЧаЮТ№ЃПШєПЩвдЃЌЧыжБНгаДГіЁЯBDAЕФЖШЪ§ЃЎШєВЛПЩвдЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁвЊОгЊвЛжжаТЩЯЪаЕФЮФОпЃЌНјМлЮЊ20дЊЈMМўЃЎЪдЯњНзЖЮЗЂЯжЃКЕБЯњЪлМлЮЊ25дЊЈMМўЪБЃЌУПЬьЕФЯњЪлСПЪЧ250МўЃЌЯњЪлМлУПЩЯеЧ1дЊЃЌУПЬьЕФЯњЪлСПОЭМѕЩй10МўЃЎ
ЃЈ1ЃЉаДГіЩЬГЁЯњЪлетжжЮФОпЃЌУПЬьЫљЕУЕФЯњЪлРћШѓ![]() ЃЈдЊЃЉгыЯњЪлЕЅМл
ЃЈдЊЃЉгыЯњЪлЕЅМл![]() ЃЈдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ2ЃЉЧѓЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌИУЮФОпУПЬьЕФЯњЪлРћШѓзюДѓЃП
ЃЈ3ЃЉдкБЃжЄЯњЪлСПОЁПЩФмДѓЕФЧАЬсЯТЃЌИУЩЬГЁЯыЛёЕУУПЬь2000дЊЕФРћШѓЃЌгІИУНЋЯњЪлМлЖЈЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌШєABCDЕФжмГЄЮЊ22 cmЃЌACЃЌBDЯрНЛгкЕуOЃЌЁїAODЕФжмГЄБШЁїAOBЕФжмГЄаЁ3 cmЃЌдђABЃН________ЁЃ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com