
����Ŀ����ͼ������ABC�У�AB=AC=2����B=��C=40������D���߶�BC���˶���D����B��C�غϣ�������AD������ADE=40����DE���߶�AC��E��
��1������BDA=115��ʱ����EDC=______������DEC=______������D��B��C�˶�ʱ����BDA��______��������������С������
��2����DC���ڶ���ʱ����ABD�ա�DCE����˵�����ɣ�
��3���ڵ�D���˶������У���ADE����״�����ǵ����������������ԣ���ֱ��д����BDA�Ķ������������ԣ���˵�����ɣ�

���𰸡���1��25�㣬115�㣬С����2����DC=2ʱ����ABD�ա�DCE�����ɼ���������3��������.
��������
��1�����ݡ�BDA=115���Լ���ADE=40�������ɵó���EDC=180��-��ADB-��ADE�����������DEC�Ķ�����
��2����DC=2ʱ�����á�DEC+��EDC=140������ADB+��EDC=140���������ADB=��DEC��������AB=DC=2�����ɵó���ABD�ա�DCE��
��3������BDA�Ķ���Ϊ110����80��ʱ����ADE����״�ǵ��������Σ�
�⣺��1����EDC=180��-��ADB-��ADE=180��-115��-40��=25����
��DEC=180��-��EDC-��C=180��-40��-25��=115����
��BDA����
�ʴ�Ϊ��25����115����С��
��2����DC=2ʱ����ABD�ա�DCE��
���ɣ��ߡ�C=40����
���DEC+��EDC=140����
�֡ߡ�ADE=40����
���ADB+��EDC=140����
���ADB=��DEC��
�֡�AB=DC=2��
���ABD�ա�DCE��AAS����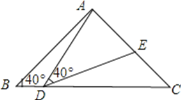
��3������BDA�Ķ���Ϊ110����80��ʱ����ADE����״�ǵ��������Σ�
���ɣ��ߡ�BDA=110��ʱ��
���ADC=70����
�ߡ�C=40����
���DAC=70������AED=��C+��EDC=30��+40��=70����
���DAC=��AED��
���ADE����״�ǵ��������Σ�
�ߵ���BDA�Ķ���Ϊ80��ʱ��
���ADC=100����
�ߡ�C=40����
���DAC=40����
���DAC=��ADE��
���ADE����״�ǵ��������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
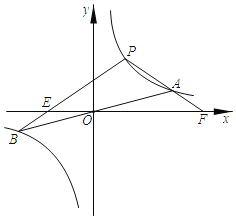
����Ŀ����ͼ��˫����y1��![]() ��ֱ��y2��
��ֱ��y2��![]() ��ͼ����A��B���㣮��֪��A������Ϊ��4��1������P��a��b����˫����y1��
��ͼ����A��B���㣮��֪��A������Ϊ��4��1������P��a��b����˫����y1��![]() �ϵ�����һ�㣬��0��a��4��
�ϵ�����һ�㣬��0��a��4��
��1���ֱ����y1��y2�ĺ�������ʽ��
��2������PA��PB���õ���PAB����4a��b����������ABP�������
��3������P��˫����y1��![]() ���˶�ʱ����PB��x���ڵ�E���ӳ�PA��x���ڵ�F���ж�PE��PF�Ĵ�С��ϵ����˵�����ɣ�
���˶�ʱ����PB��x���ڵ�E���ӳ�PA��x���ڵ�F���ж�PE��PF�Ĵ�С��ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
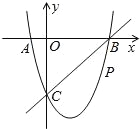
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y=x2+bx+c��ͼ����x�ύ��A��B���㣬A����ԭ����࣬B�������Ϊ��4��0������y�ύ��C��0����4���㣬��P��ֱ��BC�·�����������һ���㣮
��1����������κ����ı���ʽ��
��2������PO��PC��������POC��CO���ۣ��õ��ı���POP��C����ô�Ƿ���ڵ�P��ʹ�ı���POP��CΪ���Σ������ڣ��������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
��3������P�˶���ʲôλ��ʱ���ı���ABPC�������������ʱP���������ı���ABPC����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y��ax2��bx��c��a��0���Ķ���ΪC��1��4������x����A��B���㣬��y���ڵ� D�����е�B������Ϊ��3��0��.
��1���������ߵĽ���ʽ��
��2����ͼ2������A��ֱ���������߽��ڵ�E����y���ڵ�F�����е�E�ĺ�����Ϊ2����ֱ��PQΪ�����ߵĶԳ��ᣬ��GΪֱ��PQ�ϵ�һ���㣬��x�����Ƿ����һ��H��ʹD��G��H��F�ĵ���Χ�ɵ��ı����ܳ���С�������ڣ���������Сֵ����G��H�����ꣻ�������ڣ���˵������.
��3����ͼ3�������������Ƿ����һ��T������T��x��Ĵ��ߣ�����Ϊ��M������M��MN��BD�����߶�AD�ڵ�N������MD��ʹ��DNM�ס�BMD�������ڣ������T�����ꣻ�������ڣ���˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ѧ��ȤС���У������������λͬѧ�������ͼ��ʾ������ת������Ϸ��ÿ��ת�̱��ֳ������ȵļ������Σ�����ÿ�����������ڱ������֣�����Ϸ�������£����˷ֱ�ͬʱת���ס���ת�̣�ת��ֹͣ����ָ����ָ������������С��12���������ʤ����ָ����ָ�����������͵���12����Ϊƽ�֣���ָ����ָ�����������ʹ���12����������ʤ����ָ��ͣ�ڵȷ����ϣ���תһ�Σ�ֱ��ָ��ָ��ijһ����Ϊֹ����
��1�������б�����״ͼ�ķ�����ʾ��������Ϸ�������͵����п��ܵĽ����
��2���ֱ���������������ʤ�ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ȫУ1800��ѧ����ѧУ���õ���١����ࡢ�ܲ�������ӵȿ����������Ŀ��ϲ���������ȫУ��Χ�������ȡ��������ѧ������������ϲ����������Ŀ��ÿ��ֻѡһ��������ʾ����飬�����ݽ�����ͳ�Ʋ����Ƴ�����ͼ��ʾ��Ƶ���ֲ�ֱ��ͼ������ͳ��ͼ��������������
��1����ȫƵ���ֲ�ֱ��ͼ��
��2��������ͳ��ͼ�б�ʾ�����������Ŀ����Բ�ĽǵĶ�����
��3�����Ƹ�У1800��ѧ�����ж�������ϲ��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͨ��������롢������չ�о�������Ŀ���ɴﵽ��һ��֪һ���Ŀ�ģ�������һ��������
ԭ������ͼ������![]() �ֱ���������
�ֱ���������![]() �ı�
�ı�![]() ����
���� ![]() ������
������![]() ����
����![]() ����˵�����ɣ�
����˵�����ɣ�

��1��˼·����
��Ϊ![]() ������
������![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת90����
��ʱ����ת90����![]() ����ʹ
����ʹ![]() ��
��![]() �غϣ���Ϊ
�غϣ���Ϊ![]() ������
������![]() ����
����![]() ���ߣ�
���ߣ�
���� ����֤![]() ����
����![]() .��֤����
.��֤����
��2���������
��ͼ�����ı���![]() ����
���� ![]() ��
�� ![]() ����
����![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ����
���� ![]() .��
.��![]() ������ֱ������
������ֱ������![]() ��
��![]() ���������ϵʱ��
���������ϵʱ�� ![]() ��Ȼ��������֤����
��Ȼ��������֤����
��3��������չ
��ͼ������![]() ����
���� ![]() ����
����![]() ���ڱ�
���ڱ�![]() ������
������![]() .����
.����![]() Ӧ����ĵ�����ϵ����д��֤�����̣�
Ӧ����ĵ�����ϵ����д��֤�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�P�ǶԽ���BD�ϵ�һ�㣬��E��AD���ӳ����ϣ��ҡ�PAE=��E��PE��CD�ڵ�F��

��1����֤��PC=PE��
��2�����CPE�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��![]() ��
��![]() ��һԲ��ֱ��a��b�ֱ���A��B��C��D�ĵ㣬��P��Բ�ϵ�һ�����㣬����PA��PC.
��һԲ��ֱ��a��b�ֱ���A��B��C��D�ĵ㣬��P��Բ�ϵ�һ�����㣬����PA��PC.
(1)��ͼ1��ֱ��д����PAB����PCD����P֮���������ϵΪ�� �� ��
(2)��ͼ2��ֱ��д����PAB����PCD����P֮���������ϵΪ�� ��
(3)��ͼ3����֤����P����PAB+��PCD��
(4)��ͼ4��ֱ��д����PAB����PCD����P֮���������ϵΪ �� ��.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com