
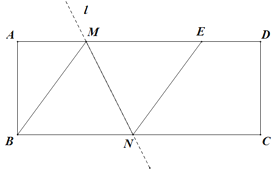
【题目】如图,在矩形ABCD中,AB=4,AD=10,点E在AD边上,已知B、E两点关于直线l对称,直线l分别交AD、BC边于点M、N,连接BM、NE.
(1)求证:四边形BMEN是菱形;
(2)若DE=2,求NC的长.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
消费卡 | 消费方式 |
普通卡 | 35元/次 |
白金卡 | 280元/张,凭卡免费消费10次再送2次 |
钻石卡 | 560元/张,凭卡每次消费不再收费 |
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用
(Ⅰ)若每年去该健身中心6次,应选择哪种消费方式更合算?
(Ⅱ)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
(Ⅲ)若某位顾客每年去该健身中心健身至少18次,请通过计算帮助这位顾客选择最合算的消费方式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,足球是世界上第一大运动,你热爱足球运动吗?已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一队共踢了30场比赛,负了9场,共得47分,那么这个队胜了( )
A. 10场 B. 11场 C. 12场 D. 13场
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=![]() 4x+4与x、y轴分别相交于点A、B,四边形ABCD是正方形,抛物线
4x+4与x、y轴分别相交于点A、B,四边形ABCD是正方形,抛物线![]() 过C,D两点,且C为顶点,则a的值为_______.
过C,D两点,且C为顶点,则a的值为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】百货商店销售某种冰箱,每台进价2500元。市场调研表明:当销售价为2900元时,平均每天能售出8台;每台售价每降低10元时,平均每天能多售出1台。(销售利润=销售价—进价)
(1)如果设每台冰箱降价x元,那么每台冰箱的销售利润为 元,平均每天可销售冰箱 台;(用含x的代数式表示)
(2)商店想要使这种冰箱的销售利润平均每天达到5600元,且尽可能地清空冰箱库存,每台冰箱的定价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC为矩形,点B坐标为(4,2),A,C分别在x轴,y轴上,点F在第一象限内,OF的长度不变,且反比例函数![]() 经过点F.
经过点F.
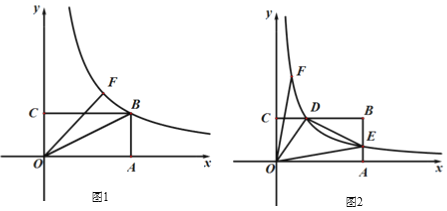
(1)如图1,当F在直线y = x上时,函数图象过点B,求线段OF的长.
(2)如图2,若OF从(1)中位置绕点O逆时针旋转,反比例函数图象与BC,AB相交,交点分别为D,E,连结OD,DE,OE.
①求证:CD=2AE.
②若AE+CD=DE,求k.
③设点F的坐标为(a,b),当△ODE为等腰三角形时,求(a+b)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
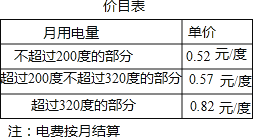
【题目】为了加强公民的节约意识,我市出台阶梯电价计算方案:居民生活用电将月用电量分为三档,第一档为月用电量200度(含)以内,第二档为月用电量200~320度(含),第三档为月用电量320度以上.这三个档次的电价分别为:第一档0.52元/度,第二档0.57元/度,第三档0.82元/度.
若某户居民1月份用电250度,则应收电费:0.52×200+0.57×(250﹣200)=132.5元.
(1)若某户居民10月份电费78元,则该户居民10月份用电_______度;
(2)若该户居民2月份用电340度,则应缴电费_______元;
(3)用x(度)来表示月用电量,请根据x的不同取值范围,用含x的代数式表示出月用电费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结 合.研究数轴我们发现了许多重要的规律:若数轴上点 A、点 B 表示的数分别为 a、b,则A、B 两点之间的距离 AB= ![]() ,线段 AB 的中点表示的数为
,线段 AB 的中点表示的数为![]() .
.
【问题情境】如图,数轴上点A表示的数为-2,点B表示的数为8,点P从点 A 出发, 以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒 2个单 位长度的速度向左匀速运动,设运动时间为t秒(t>0).
【综合运用】(1) 填空:
①A、B两点之间的距离AB=__________,线段AB的中点表示的数为_______;
②用含t的代数式表示:t秒后,点P表示的数为_______;点Q表示的数为_____.
(2) 求当t为何值时,P、Q 两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点 P在运动过程中,线段MN的长度是否发 生变化?若变化,请说明理由;若不变,请求出线段MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校派相同人数的优秀学生,参加县教育局举办的中小学生美文诵读决赛。比赛结束后,发现学生成绩分别是7分、8分、9分或10分(满分10分),核分员依据统计数据绘制了如下尚不完整的统计图表。根据这些材料,请你回答下列问题:
甲校成绩统计表 | ||||
成绩 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 | 8 | |
(1)在图①中,“7分”所在扇形的圆心角等于_______
(2)求图②中,“8分”的人数,并请你将该统计图补充完整。


(3)经计算,乙校学生成绩的平均数是8.3分,中位数是8分。请你计算甲校学生成绩的平均数、中位数,并从平均数和中位数的角度分析哪个学校的成绩较好?
(4)如果教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com