
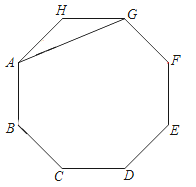
【题目】如图,AG是正八边形ABCDEFGH的一条对角线.
(1)在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由;
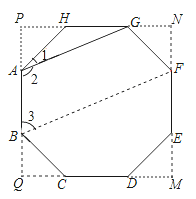
(2)两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,若AB=2,求四边形PQMN的面积.
【答案】(1)BF∥AG.理由见解析;(2)![]() .
.
【解析】试题分析: (1)利用已知得出正八边形,它的内角都为135°,再利用正八边形ABCDEFGH关于直线BF对称,得出∠2+∠3=180°,进而得出答案,
(2)根据题意得出△PAH≌△QCB≌△MDE,则PA=QB=QC=MD,即PQ=QM,故四边形PQMN是正方形,进而求出PQ的长即可得出答案.
试题解析(1)连接BF,则有BF∥AG,
理由如下:
∵ABCDEFGH是正八边形,
∴它的内角都为135°,
又∵HA=HG,
∴∠1=22.5°,
从而∠2=135°﹣∠1=112.5°,
由于正八边形ABCDEFGH关于直线BF对称,
∴∠3=![]()
![]() 135°=67.5°
135°=67.5°
即∠2+∠3=180°,故BF∥AG,
(2)根据题设可知∠PHA=∠PAH=45°,
∴∠P=90°,同理可得∠Q=∠M=90°,
∴四边形PQMN是矩形.
又∵∠PHA=∠PAH=∠QBC=∠QCB=∠MDE=∠MED=45°,AH=BC=DE,
∴△PAH≌△QCB≌△MDE,
∴PA=QB=QC=MD,即PQ=QM,
故四边形PQMN是正方形.
在Rt△PAB中,
∵∠PAH=45°,AB=2,
∴ PA=AB![]() sin45°=2
sin45°=2![]() ,
,
∴ PQ=PA+AB+BQ=![]() +2+
+2+![]() =2
=2![]() +2,
+2,
故四边形PQMN的面积 =![]() =12+8
=12+8![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k为常数,k≠0)的图象经过点A(2,3).
(k为常数,k≠0)的图象经过点A(2,3).
(1)k的值为______ ;
(2)判断点B(-1,6)是否在这个函数的图象上,并说明理由;
(3)当x<3时,直接写出y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当∠BAD=15°时,BC∥DE,则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为( )

A.60°和135°B.45°、60°、105°、135°C.30°和45°D.以上都有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 和
和![]() 两点.
两点.
观察图象可知:①当![]() 或
或![]() 时,
时,![]() ;②当
;②当![]() 或
或![]() 时,
时,![]() ,即通过观察函数的图象,可以得到不等式
,即通过观察函数的图象,可以得到不等式![]() 的解集.
的解集.
有这样一个问题:求不等式![]() 的解集.
的解集.
某同学根据学习以上知识的经验,对求不等式![]() 的解集进行了探究.
的解集进行了探究.
下面是他的探究过程,请将(![]() )、(
)、(![]() )、(
)、(![]() )补充完整:
)补充完整:
(![]() )将不等式按条件进行转化:
)将不等式按条件进行转化:
当![]() 时,原不等式不成立.
时,原不等式不成立.
当![]() 时,原不等式可以转化为
时,原不等式可以转化为![]() .
.
当![]() 时,原不等式可以转化为
时,原不等式可以转化为![]() .
.
(![]() )构造函数,画出图象.
)构造函数,画出图象.
设![]() ,
,![]() ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
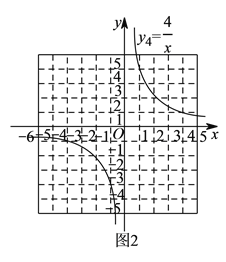
双曲线![]() 如图
如图![]() 所示,请在此坐标系中画出抛物线
所示,请在此坐标系中画出抛物线![]() .(不用列表)
.(不用列表)
(![]() )确定两个函数图象公共点的横坐标.
)确定两个函数图象公共点的横坐标.
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足![]() 的所有
的所有![]() 的值为__________.
的值为__________.
(![]() )借助图象,写出解集.
)借助图象,写出解集.
结合(![]() )的讨论结果,观察两个函数的图象可知:不等式
)的讨论结果,观察两个函数的图象可知:不等式![]() 的解集为__________.
的解集为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:FE⊥AB;
(2)当EF=6,![]() =
=![]() 时,求DE的长.
时,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
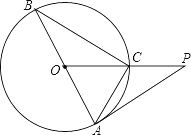
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,∠BAC=2∠B,⊙O的切线AP与OC的延长线相交于点P,若PA= 6![]() cm,求AC的长.
cm,求AC的长.
四、综合题(10分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校随机抽取部分学生,就“学习习惯”进行调查,将“对自己做错题进行整理、分析、改正”(选项为:很少、有时、常常、总是)的调查数据进行了整理,绘制成部分统计图如下:

请根据图中信息,解答下列问题:
(1)该调查的样本容量为________, ![]() =________%,
=________%, ![]() =________%,“常常”对应扇形的圆心角的度数为__________;
=________%,“常常”对应扇形的圆心角的度数为__________;
(2)请你补全条形统计图;
(3)若该校有3200名学生,请你估计其中“总是”对错题进行整理、分析、改正的
学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在“圣诞节”来临前夕,购进一种品牌巧克力,每盒进价是![]() 元.超市规定每盒售价不得少于
元.超市规定每盒售价不得少于![]() 元,根据以往销售经验发现;当售价定为每盒
元,根据以往销售经验发现;当售价定为每盒![]() 元时,每天可以卖出
元时,每天可以卖出![]() 盒,每盒售价提高
盒,每盒售价提高![]() 元,每天要少卖出
元,每天要少卖出![]() 盒.
盒.
(![]() )试求出每天的销售量
)试求出每天的销售量![]() (盒)与每盒售价
(盒)与每盒售价![]() (元)之间的函数关系式.
(元)之间的函数关系式.
(![]() )当每盒售价定为多少元时,每天销售的利润
)当每盒售价定为多少元时,每天销售的利润![]() (元)最大?最大利润是多少?
(元)最大?最大利润是多少?
(![]() )为稳定物价,有关管理部门限定:这种巧克力的每盒售价不得高于
)为稳定物价,有关管理部门限定:这种巧克力的每盒售价不得高于![]() 元.如果超市想要每天获得不低于
元.如果超市想要每天获得不低于![]() 元的利润,那么超市每天至少销售巧克力多少盒?
元的利润,那么超市每天至少销售巧克力多少盒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com